SOLUTION: the hypotenuse of a right triangle is twice as long as one of the legs and 6 inches longer than the other. what are the lengths of the sides of the triangle

Algebra ->  Triangles -> SOLUTION: the hypotenuse of a right triangle is twice as long as one of the legs and 6 inches longer than the other. what are the lengths of the sides of the triangle      Log On


   

Question 212135: the hypotenuse of a right triangle is twice as long as one of the legs and 6 inches longer than the other. what are the lengths of the sides of the triangle
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
The hypotenuse of a right triangle is twice as long as one of the legs and 6 inches longer than the other. what are the lengths of the sides of the triangle

Step 1. Let x be length of one of the legs. Then x+6 is the length of the other leg. And length of hypotenuse is 2x.

Step 2. Pythagorean Theorem. Sum of the squares of the legs is equal to the square of the hypotenuse.

x%5E2%2B%28x%2B6%29%5E2=%282x%29%5E2

Simplify right side,

x%5E2%2B%28x%2B6%29%5E2=4x%5E2

Subtract x^2 from both sides

x%5E2%2B%28x%2B6%29%5E2-x%5E2=4x%5E2-x%5E2

x%5E2%2B%28x%2B6%29%5E2-x%5E2=3x%5E2

Simplify left side and multiply out the square term of x+6

x%5E2%2B12x%2B36=3x%5E2

Subtract the left side of equation on both sides by itself to get zero on the left side. That is

x%5E2%2B12x%2B36-%28x%5E2%2B12x%2B36%29=3x%5E2-%28x%5E2%2B12x%2B36%29

Simplifying both sides of equation yields
0=2x%5E2-12x-36

Step 3. This is now a quadratic equation where we can use the quadratic formula.
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
where a=2, b=-12, c=-36

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 2x%5E2%2B-12x%2B-36+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-12%29%5E2-4%2A2%2A-36=432.

Discriminant d=432 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--12%2B-sqrt%28+432+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-12%29%2Bsqrt%28+432+%29%29%2F2%5C2+=+8.19615242270663
x%5B2%5D+=+%28-%28-12%29-sqrt%28+432+%29%29%2F2%5C2+=+-2.19615242270663

Quadratic expression 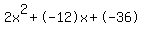2x%5E2%2B-12x%2B-36 can be factored:
2x%5E2%2B-12x%2B-36+=+2%28x-8.19615242270663%29%2A%28x--2.19615242270663%29
Again, the answer is: 8.19615242270663, -2.19615242270663. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+2%2Ax%5E2%2B-12%2Ax%2B-36+%29




Step 4. Pick the positive number since we have only positive lengths. In this case, it's 8.196. so
x=8.196 Length of one leg

x%2B6=14.196 Length of other Leg

2x=28.392 Length of hypotenuse.

You can use the Pythagorean Theorem to check if its close to verify your answer.

For Step-By-Step Videos on Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra.

For more info, contact Professor John Santiago at john@e-liteworks.com