Question 210922This question is from textbook Analytic Trigonometry
: Question #33 asked: From the sunroof of Janet's apartment building, the angle of depression to the base of an office building is 51.4 degrees and the angle of elevation to the top of the office building is 43.2 degrees. If the office building is 847 ft high, how far apart are the two buildings and how high is the apartment building?
My answer:

d=386 ft - the buildings are about 386 feet apart.

h=484 ft - the apartment building is about 484 feet tall.
***FIGURE FOR #33 LOOKS MORE LIKE THIS:***
______________/|===========|
____________/__|===========|
__________/____|===========|
________/)43.2__|===========|
=======|---------|===========|847 ft
=======|\)51.4__|===========|
=======|_\_____|===========|
=======|__\____|===========|
=======|___\___|===========|
=======|____\__|===========|
=======|_____\_|===========|
***TWO BUILDINGS NEXT TO EACHOTHER WITH A TRIANGLE BETWEEN THEM***
-------------My question is:-------------
34. Surveying:
(A) Using the figure, show that 
_____/|\
____/_|__\
___/__|____\
__/___|h_____\
_/____|________\
/_a)__|]_______(b_\
|--------- d ---------|
I started with  and then multiplied and then multiplied 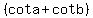 to both sides and got to both sides and got  , I somehow got lost after that. , I somehow got lost after that.
Then there is the second part:
(B) Use the results in part (A) to find the distance between the two buildings in Problem 33.
This question is from textbook Analytic Trigonometry
Found 2 solutions by Theo, jdmccarty:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let angle A be the angle of elevation. This would be 43.2 degrees.
let angle B be the angle of depression. This would be 51.4 degrees.
let d be the distance between the buildings.
let h be the height of the office building.
let x be the height of the building from the point of observation up to the angle of elevation.
let y be the height of the building from the point of observation down. to the angle of depression.
-----
tan(A) = x/d
-----
tan(B) = y/d
-----
x + y = h = 847
-----
x = d*tan(A)
y = d*tan(B)
-----
847 = d*tan(A) + d*tan(B)= d*(tan(A) + tan(B))
-----
solving for d, you got:
d = 847 / (tan(A) + tan(B))
-----
this became:
d = 847 / (tan(43.2) + tan(51.6))
which became:
d = 384.8690563
which became:
d = 385 feet to the nearest foot.
-----
from that you were able to derive x and y.
-----
the second part of this is asking you to show that h = d/(cot(A) + cot(B))
-----
i don't think this equation is accurate.
here's my reasoning.
from h = d * (tan(A) + tan(B)) you were able to derive d = h / (tan(A) + tan(B)) and get a solution that made sense.
-----
from that same equation, i could NOT derive:
h = d/(cot(A) + cot(B))
-----
i assumed that equation was right, and could NOT derive a known h from a known d and a known A and a known B.
-----
in other words, that equation is not accurate.
-----
from h = d * (tan(A) + tan(B)) i was able to derive:
h = d/cot(A) + d/cot(B) which i proved WAS accurate by substituting known values for d, h, A, and B.
-----
taking the known equation of h = d * (tan(A) + tan(B)), the best i could do was:
h = d (cot(A) + cot(B))/(cot(A)*cot(B))
this was equivalent to:
h = d/cot(A) + d/cot(B)
-----
in other words, i don't think you have the right equation for problem number 34.
-----
i also went back to your original problem and solved for h using cotangent rather than tangent.
the equation i got was:
h = d/cot(A) + d/cot(B) which is NOT equal to d/(cot(A) + cot(B))
----
P.S.
a picture of how i viewed this problem can be found on my website at:
http://theo.x10hosting.com/
look for problem number 210922.
if it's not there, wait 30 minutes and try again.
-----
Answer by jdmccarty(1)   (Show Source): (Show Source):
You can put this solution on YOUR website! Okay, here we go:

COT is simply the opposite of TAN, correct? this means that: TAN=opp/adj; COT=adj/opp
So;
(A) Using the figure, show that 
_____/|\
____/_|__\
___/__|____\
__/___|h_____\
_/____|________\
/_a)__|]_______(b_\
__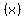 __|___ __|___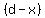
|---------  ---------| ---------|
Notice that we split  between the two triangles with between the two triangles with  and and 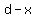 That is where we will begin That is where we will begin
We start by recognizing that;
cota=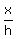
cotb=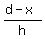
Plug in our new values to the original equation and:

Simplify, the x cancels and:

In order to go any further, we need to realize that 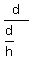 = = 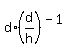 and since and since  is really is really 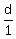 we end up with: we end up with:

Negative exponents aren't as scary as they seem, we simply use the inverse, and get: 
Simplify and find that  cancels and our answer is: cancels and our answer is: 
____________________________NEXT PART____________________________
(B) You did this in the last problem, #33 only used TAN. Remember that COT is the inverse of TAN and to find COT on the calculator, just divide 1 by TAN.
But you are on the wrong side of the triangles! Well, we know that a triangle totals 180 degrees and a right triangle uses a 90 degree; leaving us with two other angles to add up to 90 degrees and we have one angle for each triangle already! What were they?
43.2 degrees and 51.4 degrees
Take one angle and subtract it from the remaining 90 degrees left over in our triangle, then repeat with the other:
cota= and cotb= and cotb=
Now get out your calculators and start punching digits.
1/tan(46.8)~.94 and 1/tan(38.6)~1.25 (both to the nearest penny)
Back to our original problem, plug in the new numbers and we get:
 The buildings are still about 386 feet apart. The buildings are still about 386 feet apart.
|
|
|