SOLUTION: sorry I already ask this question but i cannot find it again (x+ 1/x)^2 -2(x+ 1/x)+1=0 this part of equation in quadratic form I already got an answer x^4-2x^3+3x^2-2x+1=0 But

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: sorry I already ask this question but i cannot find it again (x+ 1/x)^2 -2(x+ 1/x)+1=0 this part of equation in quadratic form I already got an answer x^4-2x^3+3x^2-2x+1=0 But      Log On


   

Question 210323This question is from textbook COLLEGE ALGEBRA
: sorry I already ask this question but i cannot find it again
(x+ 1/x)^2 -2(x+ 1/x)+1=0 this part of equation in quadratic form
I already got an answer x^4-2x^3+3x^2-2x+1=0 But i got stuck here i dont know what to do next
thank you for your help This question is from textbook COLLEGE ALGEBRA

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
%28x%2B+1%2Fx%29%5E2+-2%28x%2B+1%2Fx%29%2B1=0 Start with the given equation.


Take note that the term 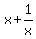x%2B1%2Fx is being repeated here. So one way to simplify this equation (for now) is to do a simple substitution


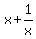So let z=x%2B1%2Fx. So this means that z%5E2=%28x%2B1%2Fx%29%5E2


z%5E2-2z%2B1=0 Replace each instance of x%2B1%2Fx with 'z'


Now we have a much simpler equation to solve for.


Notice that the quadratic 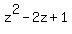z%5E2-2z%2B1 is in the form of Az%5E2%2BBz%2BC where A=1, B=-2, and C=1


Let's use the quadratic formula to solve for "z":


z+=+%28-B+%2B-+sqrt%28+B%5E2-4AC+%29%29%2F%282A%29 Start with the quadratic formula


z+=+%28-%28-2%29+%2B-+sqrt%28+%28-2%29%5E2-4%281%29%281%29+%29%29%2F%282%281%29%29 Plug in A=1, B=-2, and C=1


z+=+%282+%2B-+sqrt%28+%28-2%29%5E2-4%281%29%281%29+%29%29%2F%282%281%29%29 Negate -2 to get 2.


z+=+%282+%2B-+sqrt%28+4-4%281%29%281%29+%29%29%2F%282%281%29%29 Square -2 to get 4.


z+=+%282+%2B-+sqrt%28+4-4+%29%29%2F%282%281%29%29 Multiply 4%281%29%281%29 to get 4


z+=+%282+%2B-+sqrt%28+0+%29%29%2F%282%281%29%29 Subtract 4 from 4 to get 0


z+=+%282+%2B-+sqrt%28+0+%29%29%2F%282%29 Multiply 2 and 1 to get 2.


z+=+%282+%2B-+0%29%2F%282%29 Take the square root of 0 to get 0.


z+=+%282+%2B+0%29%2F%282%29 or z+=+%282+-+0%29%2F%282%29 Break up the expression.


z+=+%282%29%2F%282%29 or z+=++%282%29%2F%282%29 Combine like terms.


z+=+1 or z+=+1 Simplify.


So the only solution in terms of 'z' is z+=+1


However, we want to solve for 'x' (not 'z'). But do recall that we let z=x%2B1%2Fx


z=x%2B1%2Fx Start with the given equation.


1=x%2B1%2Fx Plug in the solution (in terms of 'z') z=1


x=x%5E2%2B1 Multiply EVERY term by the LCD 'x' to clear out the fraction.


0=x%5E2-x%2B1 Subtract 'x' from both sides.


Notice that the quadratic 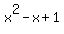x%5E2-x%2B1 is in the form of Ax%5E2%2BBx%2BC where A=1, B=-1, and C=1


Let's use the quadratic formula to solve for "x":


x+=+%28-B+%2B-+sqrt%28+B%5E2-4AC+%29%29%2F%282A%29 Start with the quadratic formula


x+=+%28-%28-1%29+%2B-+sqrt%28+%28-1%29%5E2-4%281%29%281%29+%29%29%2F%282%281%29%29 Plug in A=1, B=-1, and C=1


x+=+%281+%2B-+sqrt%28+%28-1%29%5E2-4%281%29%281%29+%29%29%2F%282%281%29%29 Negate -1 to get 1.


x+=+%281+%2B-+sqrt%28+1-4%281%29%281%29+%29%29%2F%282%281%29%29 Square -1 to get 1.


x+=+%281+%2B-+sqrt%28+1-4+%29%29%2F%282%281%29%29 Multiply 4%281%29%281%29 to get 4


x+=+%281+%2B-+sqrt%28+-3+%29%29%2F%282%281%29%29 Subtract 4 from 1 to get -3


x+=+%281+%2B-+sqrt%28+-3+%29%29%2F%282%29 Multiply 2 and 1 to get 2.


x+=+%281+%2B-+i%2Asqrt%283%29%29%2F%282%29 Simplify the square root


x+=+%281%2Bi%2Asqrt%283%29%29%2F%282%29 or x+=+%281-i%2Asqrt%283%29%29%2F%282%29 Break up the expression.


============================================================================
Answer:


So the solutions (in terms of x) are x+=+%281%2Bi%2Asqrt%283%29%29%2F%282%29 or x+=+%281-i%2Asqrt%283%29%29%2F%282%29


Note: since the degree of 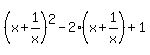%28x%2B+1%2Fx%29%5E2+-2%28x%2B+1%2Fx%29%2B1 turns out to be 4, this means that there are really 4 solutions. So what happened? The twist is that each solution is counted twice. You'll most likely hear that these solutions are of multiplicity 2.