Question 208999: In a chess match, a win counts 1 point, a draw counts 1/2 point, and a loss counts 0 points. After 15 games, the winner was 4 points ahead of the loser. How many points did the loser have?
Found 2 solutions by Theo, MathTherapy:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! this is a little tricky, but it appears the answer is as follows:
-----
A wins 4 and draws 11.
A score will be 4 + 11/2 = 19/2.
B score will be 11/2.
Net Score is: 19/2 minus 11/2 equal 4.
The winner scored 19/2 and the loser scores 11/2.
-----
A wins 5 and loses 1 and draws 9.
A score will be 5 + 9/2 = 19/2
B score will be 1 + 9/2 = 11/2
Net Score is: 19/2 minus 11/2 equal 4.
The winner scored 19/2 and the loser scores 11/2.
-----
A wins 6 and loses 2 and draws 7.
A score will be 6 + 7/2 = 19/2
B score will be 2 + 7/2 = 11/2
Net Score is: 19/2 minus 11/2 equal 4.
The winner scored 19/2 and the loser scores 11/2.
-----
A wins 7 and loses 3 and draws 5.
A score will be 7 + 5/2 = 19/2
B score will be 3 + 5/2 = 11/2
Net Score is: 19/2 minus 11/2 equal 4.
The winner scored 19/2 and the loser scores 11/2.
-----
A wins 8 and loses 4 and draws 3.
A score will be 8 + 3/2 = 19/2
B score will be 4 + 3/2 = 11/2
Net Score is: 19/2 minus 11/2 equal 4.
The winner scored 19/2 and the loser scores 11/2.
-----
A wins 9 and loses 5 and draws 1.
A score will be 9 + 1/2 = 19/2
B score will be 5 + 1/2 = 11/2
Net Score is: 19/2 minus 11/2 equal 4.
The winner scored 19/2 and the loser scores 11/2.
-----
stops here because 10 and 6 = 16 which is greater than 15.
-----
in all of these, the winner scores 19/2 total and the loser scores 11/2 total making the difference between winner and loser = 4
-----
19/2 minus 11/2 = 8/4 = 4
-----
your answer is the loser had 11/2 points = (5.5).
-----
the winner had 19/2 points = (9.5).
-----
if you wanted to put this in an equation, it would be as follows:
-----
let aw = number of wins for A.
let al = number of losses for A.
let ad = number of draws for A.
-----
let bw = number of wins for B.
let bl = number of losses for B.
let bd = number of draws for B.
-----
the number of draws for a will always equal the number of draws for b, so we can simply say that the number of draws for each is d.
out variables become:
aw
al
bw
bl
d
-----
since the number of games played is 15, then the equation for a becomes:
aw + al + d = 15
and the equation for b becomes:
bw + bl + d = 15
-----
the score for A is given by the equation:
(1 * aw) + (.5 * d) + (0 * al) which becomes:
the score for A = aw + .5d
-----
the score for B is given by the equation:
(1 * bw) + (.5 * d) + (0 * bl) which becomes:
the score for B = bw + .5d
-----
we know that the difference in the score between the winner and the loser is 4.
assuming A was the winner, we get:
aw + .5d = bw + .5d + 4
subtract .5d from both sides of this equation to get:
aw = bw + 4
-----
what this says is that the number of wins for A will exceed the number of wins for B by 4
-----
the score for A is given by the equation:
aw + .5*d
we know that aw + al + d = 15
we know al = bw (loss for a equals win for b)
equation becomes:
aw + bw + d = 15
we know that aw = bw + 4 from above so we get:
bw + 4 + bw + d = 15
this becomes:
2bw + d = 11
this becomes d = 11 - 2bw
-----
so if we know the number of wins for B, we can calculate the number of draws for A and B and we can calculate the number of wins for A.
-----
here's how.
equation is:
d = 11 - 2bw.
if bw = 1 then d = 9
if bw = 2 then d = 7
if bw = 3 then d = 5
if bw = 4 then d = 3
if bw = 5 then d = 1
if bw = 6 then d = -1 no good so maximum number of draws is 5.
-----
scores for B will be 1 * bw + .5 * d
but d = (11 - 2bw) which makes .5*d = (11 - 2bw)/2 so:
if we let S = score for B, we get:
S = bw + (11-2bw)/2
multiply both sides by 2 to get:
2S = 2bw + 11 - 2bw
this becomes:
2S = 11
which becomes:
S = 11/2
-----
score for B will always be 11/2 if B loses to A by 4 points.
-----
similarly, we can find the score for A.
-----
score for A equals aw + .5d
we know that:
aw + al + d = 15
we know that aw = bw + 4 which means that bw = aw - 4
using that, our equation becomes:
aw + aw - 4 + d = 15
which becomes:
2aw + d = 19
which becomes:
d = 19 - 2aw
-----
score for A is equal to aw + .5d
let S = score for A.
substituting 19 - 2aw for d, this equation becomes:
S = aw + (19 - 2aw)/2
multiply both sides by 2 to get:
2S = 2aw + 19 - 2aw
which becomes:
2S = 19
which becomes:
S = 19/2
-----
score for A will always be 19/2 if A beats B by 4 points.
-----
it's a little convoluted but it works.
-----
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website!
In a chess match, a win counts 1 point, a draw counts 1/2 point, and a loss counts 0 points. After 15 games, the winner was 4 points ahead of the loser. How many points did the loser have?
Since 15 games were played, then the total amount of accumulated points for both the winner and the loser is 15. This is because for each game, 1 point will be awarded to one, or both. For example, if the game is drawn, each party gets  a point. And, if there's a winner, then he/she gets 1 point while the loser gets 0 (zero) points.
Let the loser's amount of points, after 15 games, be L
Since the winner had 4 more points than the loser at the end of 15 games, then the winner would have: L + 4 points after 15 games
Therefore, L + L + 4 = 15
2L + 4 = 15
2L = 11
Therefore, the loser had 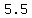 points after 15 games.
This also means that the winner would have 9.5 (5.5 + 4) points.
|
|
|
