Question 20884: Write a matrix equation equivalent to the system of equations.
9x + 9y = -9
5x - 2y = 6
Cramer's rule.
6x + 4y = -4
y = -3x - 7
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write a matrix equation equivalent to the system of equations.
9x + 9y = -9
5x - 2y = 6
we write the matrix equation as (A)*(X)=(C)..where A is the (2,2)matrix of coefficients namely,9,9,5 and -2 here.X is the (2,1) matrix of unknowns x and y and C is the constants (2,1)matrix on the right side of the eqn NAMELY -9 AND 6.you will find that from the rule for equality of matrices,the above matrix eqn.in effect means the same as that of the given equations.
(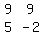 )*( )*( )=( )=(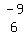 ) )
Cramer's rule.
6x + 4y = -4
y = -3x - 7
GIVING BELOW EXAMPE OF CRAMERS RULE.
My question is.... I was wondering how to do the cramer rule on a 3x3. I have found a bunch of examples and stuff, but I want to know how in the world do you find the determinants of the D, Dx, Dy.and Dz. If you could just tell me how, that would be great.
1 solutions
Answer 9496 by venugopalramana(585) About Me on 2005-11-15 10:49:54 (Show Source):
SEE THE FOLLOWING AND COME BACK IF YOU HAVE DIFFICULTY.HERE C,CX,CY,CZ REFER TO YOUR D,DX,DY,DZ...JUST A DIFFERENCE IN NOMENCLATURE.I SHOWED IN DETAIL A 2X2 DETERMINANT AND THEN IN BRIEF A 3X3 DETERMINANT
2x+y=4
3x-y=6
make a deteminant with coefficients of x (2,3)and y(1,-1) in the 2 eqns.call it C.(Actually for a determinant as you know ,the numbers are contained in vertical bars at either end like |xx|,but in the following the bars are omitted due to difficulty in depiction.you may assume the bars are present)
C=matrix(2,2,2,1,3,-1)=2*(-1)-(1*3)=-5
..now use the constants (4,6)to replace coefficients of x(2,3) in the above determinant C...call it CX..
CX=matrix(2,2,4,1,6,-1)=4*(-1)-1*6=-4-6=-10
..now use the constants (4,6)to replace coefficients of y(1,-1) in the above determinant C...call it CY..
CY=matrix(2,2,2,4,3,6)=2*6-3*4=12=12=0
..now cramers rule says that
(x/CX)=(y/CY)=(1/C)..so we get
x/(-10)=y/0=1/-5
x=-10/-5=10/5=2
y=0/-5=0
************************************
so using the above method you can do the next problem ..here due to presence of 3 variables you will get 3rd.order determinants...4 in all...namely C,CX,CY and CZ,the last formula also extends to include z ,
(x/CX)=(y/CY)=(z/CZ)=(1/C)..
but the procedure is same ..
2x+3y+ z= 5
x+y-2z= -2
-3x +z=-7 ...
...just to give you the idea
C=matrix(3,3,2,3,1,1,1,-2,-3,0,1)..and
CZ=matrix(3,3,2,3,5,1,1,-2,-3,0,7)..etc..hope you can work out the rest
|
|
|