Question 208474: I am trying to figure out a question that has 2 parts. The question is as follows:
A) What is the domain and range of the relation x +[y] = 3?
b) What is the domain and range of the function y = 2x^2-3?
Since [y] cannot be a negative number would the answer for part (a) be: (-&, 3)
For part (b) I am not quite sure bit I think it would be a union containing the square root of 2).
I am lost!
Any help would be greatly appreciated.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! use the || rather than the [].
|x| means absolute value of x.
-----
the | is the shift \
-----
PROBLEM NUMBER 1
-----
domain and range of the function x + |y| = 3
-----
-----
A) What is the domain and range of the relation x +[y] = 3?
-----
my previous answer i think was incorrect.
-----
i believe the right answer is that the domain has to be x <= 3.
the range, however, will be any real value of y simply because the absolute value of y is positive regardless if y is negative or positive.
-----
here's why.
-----
x + |y| = 3
subtract x from both sides to get:
|y| = 3 - x
-----
|y| is positive so 3 - x has to be positive.
3 - x is positive if x <= 3
-----
this makes the original equation of x + |y| valid as long as x <= 3.
-----
let x = 3, then 3 + |y| = 3 will be satisfied if y = 0.
-----
let x = 5 which is > 3.
this make 5 + |y| = 3 invalid because there is no value of y that will make the |y| = - 2 which it would have to be if the equation were to be satisfied because the absolute value of y has top be positive.
-----
so, my original answer is incorrect.
-----
the correct ansWer is:
-----
domain is all real values of x <= 3
-----
with a domain of x <= 3, the range will be:
|y| = x-3
meaning that:
y = 3-x
or:
y = - (3-x)
-----
if x = 3, then y will be 0 or -0
if x = 0, then y will be -3 or 3
if x is less than 0, then y will be a value > 3 or < -3
-----
looks like the domain is x <= 3, and the range is all real values of y
-----
let's see how that works:
-----
as long as we keep the value of x less than or equal to 3 we should be ok.
-----
FIRST
-----
let x = 3
this means that:
y = 3-3 = 0
or:
y = - (3-3) = -0
-----
if y = 0, then 3 + |0| = 3 + 0 = 3 which satisfies the original equation of x + |y| = 3
-----
if y = -0, then 3 + |-0| = 3 + 0 = 3 which satisfies the original equation of x + |y| = 3
-----
SECOND
-----
let x = 0
this means that:
y = 3-0 = 3
or:
y = - (3-0) = -3
-----
if y = 3, then 0 + |3| = 0 + 3 = 3 which satisfies the original equation of x + |y| = 3
-----
if y = -3, then 0 + |-3| = 0 + 3 = 3 which satisfies the original equation of x + |y| = 3
-----
THIRD
-----
let x = -100
this means that:
y = 3-(-100) = 103
or:
y = - (3-(-100)) = -103
-----
if y = 103, then -100 + |103| = -100 + 103 = 3 which satisfies the original equation of x + |y| = 3
-----
if y = -103, then -100 + |-103| = -100 + 103 = 3 which satisfies the original equation of x + |y| = 3
-----
so far as long as we allowed x to be smaller than or equal to 3 we were in good shape.
-----
if we allow x to be > 3 we should run into a problem.
-----
let x = 5 which is greater than 3
this means that:
y = 3-5 = -2
or:
y = - (3-5)= -(-2) = 2
-----
if y = -2, then 5 + |-2| = 5 + 2 = 7 which does NOT satisfy the original equation of x + |y| = 3.
-----
if y = 2, then 5 + |2| = 5 + 2 = 7 which does NOT satisfy the original equation of x + |y| = 3
-----
bottom line is:
-----
the domain is x <= 3
the range is y can be any real number
-----
a graph of the equation would show this to be true but you have to look at the graph only for the values of x <= 3.
you have to ignore any values of x > 3.
-----

from this graph you can see that:
when x = 3, y = 0
when x = 0, y = +/- 3
when x = -6, y = +/- 9
-----
in all cases the |y| is positive and the equation of x + |y| = 3 is satisfied as long as x <= 3
-----
PROBLEM NUMBER 2
-----
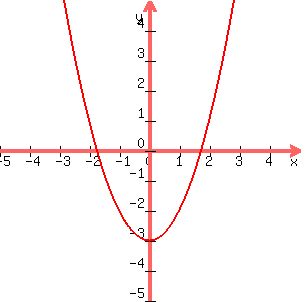
domain and range of the function y = 2x^2-3?
------
looks like any real number of x will satisfy this equation.
if x is a positive number, then y will be a positive number >= -3
if x is 0 y will be = to -3
if x is a negative number, then y will be a positive number >= -3
-----
looks like the lowest y can be is -3.
this happens when x = 0
any number of x > 0 or < 0 will result in a value of y that is greater than -3.
so:
domain is all real numbers.
range is all real numbers >= to -3
-----
graph of this equation is:
-----
-----
|
|
|