Use the leading coefficient test determine
the end behavior of the polynomial function
Here are the rules for determining end behavior on all
polynomial functions:
Find the leading term, which is the term with the
largest exponent.
1. Is the leading term's coefficient positive? Then it goes
up one the right end.
2. Is the leading terms' coefficient negative? Then it goes
down on the right end.
3. Is the leading terms' exponent even? Then it goes the same
way on the left end as it does on the right end.
4. Is the leading terms' exponent odd? Then it goes the
opposite way on the left end than it does on the right end.
Let's go thru those rules with your polynomial
Find the leading term, which is the term with the
largest exponent.
That's 
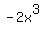1. Is the leading term's coefficient positive?
No, it's -2 and that is negative.
2. Is the leading terms' coefficient negative?
Yes, for -2 is negative.
Then it goes down on the right end.
3. Is the leading terms' exponent even?
No, it's 3 which is odd.
4. Is the leading terms' exponent odd?
Yes, for 3 is odd.
Then it goes the opposite way on the left end than
it does on the right end.
Since it goes down on the right, it goes up on the left
end.
In a nutshell, the rules are:
1. positive coefficient, up on right end.
2. negative coefficient, down on right end.
3. even power, left end same as right end.
4. odd power, left end opposite from right end.
Edwin
