Question 208387: 1. The speed of a boat in still water is 10 mph. If it travels on a river 6 miles downstream in the same amount of time it takes to travel 3 miles upstream, what is the speed of the current?
2. The speed of a boat in still water is 8 mph. If it travels 24 miles upstream and 24 miles downstream in a total of 12 hours, what is the speed of the current?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! PROBLEM NUMBER 1
-----
let b = speed of the boat in still water.
let c = speed of the current
-----
rate * time = distance
let h = time
-----
going downstream, the formula is (b + c) * h = 6
going upstream, the formula is (b - c) * h = 3
-----
since b = 10, these formula become:
(10 + c) * h = 6
and
(10 - c) * h = 3
-----
since 6 = 2 * 3, then we can substitute (10 - c) * h for 3 to get:
(10 + c) * h = (10 - c) * h * 2
-----
this formula becomes:
10h + ch = 20h - 2ch
we add 2ch to both sides and we subtract 10h from both sides to get:
3ch = 10h
we divide both sides by h to get:
3c = 10
we divide both sides by 3 to get:
c = 10/3
-----
our first equation is:
(10 + c) * h = 6
we replace c with 10/3 to get:
(10 + 10/3) * h = 6
this becomes:
(40/3) * h = 6
we multiply both sides by 3 to get:
40 * h = 18
we divide both sides by 40 to get:
h = 18/40
-----
that's our answer.
-----
to prove the answer is correct, we substitute in the original formulas:
(10 + 10/3) * 18/40 = 6
this becomes:
(40/3) * 18/40 = 6
this becomes:
18/3 = 6 which becomes 6 = 6 which is true.
-----
(10 - 10/3) * 18/40 = 3
this becomes:
(20/3) * 18/40 = 3
this becomes:
(1/3) * (18/2) = 3
this becomes:
(1/3) * 9 = 3 which becomes 3 = 3 which is true3.
-----
answer checks out so h = 18/40 is good.
-----
PROBLEM NUMBER 2
-----
b = speed of boat = 8 miles per hour
c = speed of current
f = time to go with the current
g = time to go against the current
d = distance = 24
time to go down and back = 12 hours.
-----
(b-c)*g = 24
(b+c)*f = 24
g + f = 12
-----
(b+c)*f = (b-c)*g because they both equal to 24.
-----
this expands to:
bf + cf = bg - cg
-----
since f+g = 12, then f = 12-g
-----
substitute 12-g for f in bf + cf = bg - cg to get:
b * (12 - g) + c * (12 - g) = b*g - c*g
-----
since b = 8, substitute 8 for b in equation to get:
8 * (12 - g) + c * (12 - g) = 8*g - c*g
-----
expand to get:
96 - 8g + 12c - cg = 8g - cg
-----
subtract 8g from both sides and add cg to both sides to get:
96 - 16g + 12c = 0
-----
solving for c, we get:
c = (16g - 96)/12
-----
take the original equation of (b-c) * g = 24
substitute 8 for b
substitute (16g-96)/12 for c
solve for g
-----
equation becomes:
(8 - ((16g-96)/12))*g = 24
-----
multiply both sides by 12 to get:
(96 - (16g - 96))*g = 24 * 12
which becomes:
96g - 16g^2 + 96g = 288
-----
combine like terms to get:
-16g^2 + 192g = 288
subtract 288 from both sides to get:
-16g^2 + 192g - 288 = 0
multiply both sides by -1 to get:
16g^2 - 192g + 288 = 0
divide both sides by 16 to get:
g^2 - 12g + 18 = 0
-----
use the quadratic formula to solve for g.
a factor = 1
b factor = -12
c factor = 18
quadratic formula is:
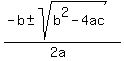
g becomes:
(12 +/- sqrt(72))/2
this turns out to be:
g = 10.24264069
or:
g = 1.757359313
-----
using these values of g and solving for c in the equation of (8-c)*g = 24, we get:
c = 5.656854249
or:
c = -5.656854249
-----
since c is the speed of the current, it can't be negative, so the only good answer is c = 5.656854249.
since this c was calculated with g = 1.757359313, that value of g is no good either.
-----
we should have all we need:
-----
we have:
g = 10.24264069
and:
c = 5.656854249
and:
f = 1.757359313 which was found by taking 12 - g since f + g equals 12.
-----
the question was what is the speed of the current and the answer is:
-----
speed of the current is c which equals 5.656854249 miles per hour.
-----
to confirm the answer is ccorrect, we substitute in the original equations.
-----
the original equation said that the boat went down stream for 24 miles and back up stream for 24 miles in a total of 12 hours.
-----
f is the time it took to get downstream.
g is the time it took to get back up stream
-----
going downstream the boat went 8 miles per hour with a current of 5.656854249 miles per hour in the same direction for a total of 13.65685425 miles per hour taking a time of 1.757359313 hours to go a distance of 24 miles.
-----
coming back upstream, the boat went 8 miles per hour against a current of 5.656854249 miles per hour in the opposite direction for a total of 2.343145751 miles per hour taking a time of 10.24264069 hours to go a distance of 24 miles.
-----
total time taken was 1.757359313 hours plus 10.24264069 hours = 12 hours.
-----
all the numbers check out so the current speed is accurate and the answer is:
speed of the current is 5.656854249 miles per hour.
-----
|
|
|