|
Question 208010This question is from textbook elementary and intermediate algebra
: determine whether each pair of equations represents parallel lines:
y=-3x+1, 6x+2y=8
This question is from textbook elementary and intermediate algebra
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! determine whether each pair of equations represents parallel lines:
y=-3x+1, 6x+2y=8
There are several ways to do this. Pick whichever way
your teacher told you to use.
Method 1: Put them both in slope-intercept form. If
their slopes are equal, but they have different
y-intercepts, then they are parallel.
Method 2: Choose any two values for x. Substitute
them both in each equation to find the
y-values corresponding to them. If the
corresponding y-values have the same non-zero
difference, then the lines are parallel.
Method 3: Put them both in general form. Then
 if
if  then they are parallel.
----------------------
Method 1: then they are parallel.
----------------------
Method 1:
 The first one is already in the slope intercept form
The first one is already in the slope intercept form
 . Get the second one in slope-intercept
form, by solving for y . Get the second one in slope-intercept
form, by solving for y
 Add
Add 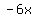 to both sides: to both sides:
 Divide every term by
Divide every term by  : :

 So the slope is the coefficient of x, which is -3
So the value of the slope
So the slope is the coefficient of x, which is -3
So the value of the slope  is the same in
both equations, but their y-intercepts are different.
Therefore the lines those equations
represent are parallel.
----------------------------------
Method 2: is the same in
both equations, but their y-intercepts are different.
Therefore the lines those equations
represent are parallel.
----------------------------------
Method 2:
 Substitite x=0 in each and solve for y:
In the first one:
Substitite x=0 in each and solve for y:
In the first one:


 In the second one:
In the second one:




 Subtract them, second y - first y =
Subtract them, second y - first y =  Substitite x=1 in each and solve for y:
In the first one:
Substitite x=1 in each and solve for y:
In the first one:



 In the second one:
In the second one:




 Subtract them, second y - first y =
Subtract them, second y - first y =  We get the same difference 3, so the lines represented
by those equations are parallel.
------------------------------------------------
Method 3:
We get the same difference 3, so the lines represented
by those equations are parallel.
------------------------------------------------
Method 3:
 Get the forst one in general form:
Get the forst one in general form:

 So the system is now:
So the system is now:
 See if the coefficients of x and y are in
the same proportion:
Is
See if the coefficients of x and y are in
the same proportion:
Is  true?
Yes it is, therefore the lines those equations
represent are parallel.
Edwin true?
Yes it is, therefore the lines those equations
represent are parallel.
Edwin
|
|
|
| |