Question 207608: A sample of 500 shoppers was selected in a large metropolitan are to determine various information concerning consumer behavior. Among the questions asked was, “Do you enjoy shopping for clothing?” Of the 240 males, 136 said yes. Of 260 females, 224 answered yes.
a) Is there evidence of a significant difference between males and females in the proportion who enjoy shopping for clothing at the 0.01 level of significance?
b) Find the p-value in (a) and interpret its meaning
c) Construct and interpret a 95% confidence interval estimate of the difference between the proportion of males and females who enjoy shopping for clothing.
d) What are your answers to (a) through (c) if 206 males enjoyed shopping for clothing?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i took info on proportions from the following website:
http://stattrek.com/Lesson3/CentralTendency.aspx?Tutorial=Stat
http://stattrek.com/Lesson3/Variability.aspx?Tutorial=Stat
-----
the mean of the sample is the number of people who said yes.
the standard deviation of the sample is 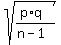 where: where:
p = probability of occurrence.
q = 1-p
-----
to the nearest 5 decimal point accuracy, the numbers appear to be:
-----
number of males = 240
number of males who said yes = 136
proportion of males who said yes = .56667 = p
q = 1 - .56667 = .43333
standard deviation of the male sample = 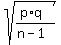 = =  = = 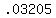
-----
number of females = 260
number of females who said yes = 224
proportion of females who said yes = .86154 = p
q = 1 - .86154 = .13846
standard deviation of the female sample = 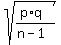 = =  = = 
-----
we can either compare the male to the female or the female to the male. we should get consistent answers.
-----
we will assume 2 tailed hypothesis testing because the difference can be high or low depending on which sample is being compared to which sample.
since we'll be doing both, you'll see what I mean.
-----
2 tailed hypothesis testing means that .01 cutoff point (called alpha) is split between the high end of the sample distribution and the low end of the sample distribution
-----
same with .05 cutoff point (called alpha).
-----
.05 cutoff point is at 95% confidence interval.
.01 cutoff point is at 99% confidence interval.
-----
you can check the pictures of the z-table calculator at the following website:
http://theo.x10hosting.com/
look for problem number 207608.1 through 207608.8 I believe.
207608.1 shows the cutoff point for .01 critical value using female sample.
207608.2 shows the cutoff point for .05 critical value using female sample.
207608.3 shows the cutoff point for .01 critical value using male sample.
207608.4 shows the cutoff point for .05 critical value using male sample.
-----
the z-table calculator can be found at the following website:
http://davidmlane.com/hyperstat/z_table.html
-----
comparing the male sample mean to the female sample distribution, we get the following:
female sample mean = .86154
female sample standard deviation = .02146
male sample mean = .56667
-----
the probability of getting a .56667 response or below is zero meaning that there is a significant statistical difference between male and female responses.
-----
you can see the results in problem number 207608.5
-----
comparing the female sample mean to the male sample distribution, we get the following:
male sample mean = .56667
male sample standard deviation = .03205
female sample mean = .86154
-----
the probability of getting a .86154 response or above is zero meaning that there is a significant statistical difference between male and female responses.
-----
you can see the results in problem number 207608.6
-----
since the numbers were off the charts in both cases, it doesn't matter whether you used a p = .01 cutoff or a p = .05 cutoff. the differences are significant either way.
-----
RESULTS OF CHANGING THE NUMBER OF MALES WHO LIKED SHOPPING FROM 136 TO 206 ARE SHOWN BELOW:
-----
if 206 males enjoyed shopping, the answers would be as follows:
-----
comparing the male sample mean to the female sample distribution, we get the following:
female sample mean = .86154
female sample standard deviation = .02146
male sample mean = .85833
-----
the probability of getting a .85833 response or below is .440548 which is well above the cutoff point meaning that there would be no significant statistical difference if 206 out of 240 males liked shopping instead of the original 136.
-----
you can see the results in problem number 207608.7
-----
comparing the female sample mean to the male sample distribution, we get the following:
male sample mean = .85833
male sample standard deviation = .02256
female sample mean = .86154
-----
the probability of getting a .86154 response or above is .443427 which is well below the cutoff point meaning that there would be no significant statistical difference if 206 out of 240 males liked shopping instead of the original 136.
-----
you can see the results in problem number 207608.8
-----
since the numbers were well within the limits in both cases, it doesn't matter whether you used a p = .01 cutoff or a p = .05 cutoff. the differences are insignificant either way as long as 206 males liked shopping rather than the original 136.
-----
i think i got this right but you should double check with some other knowledgeable person just in case.
i thought of taking the total sample mean and comparing the males and females to that but i didn't think it would say much since we wuld not be comparing them to each other but to the total population which would be comprised of both.
-----
if you go to my website and the problem number is not there, wait one hour and try again just in case i have difficulty posting.
-----
EXPLANATION OF WHAT'S ON THE WEBSITE.
-----
207608.1
female mean and standard deviation critical value of .01
shows that with a mean of .86154 and a standard deviation of .02146 and a critical cutoff value of .01, a score below .8063 or above .9168 would be a significant difference.
-----
207608.2
female mean and standard deviation critical value of .05
shows that with a mean of .86154 and a standard deviation of .02146 and a critical cutoff value of .05, a score below .8195 or above .9036 would be a significant difference.
-----
207608.3
male mean and standard deviation critical value of .01
shows that with a mean of .56667 and a standard deviation of .0325 and a critical cutoff value of .01, a score below .4841 or above .6492 would be a significant difference.
-----
207608.4
male mean and standard deviation critical value of .05
shows that with a mean of .56667 and a standard deviation of .0325 and a critical cutoff value of .05, a score below .5039 or above .6295 would be a significant difference.
-----
207608.5
comparing male mean to female mean distribution.
female mean is .86154 and female standard deviation is .02146
there is a 0 probability that a male mean score of .56667 or lower will occur.
the actual probability is greater than zero but it's too small to show.
this makes the difference between male mean scores and female mean scores very significant.
-----
207608.6
comparing female mean to male mean distribution.
male mean is .56667 and male standard deviation is .0325
there is a 0 probability that a female mean score of .86154 or higher will occur.
the actual probability is greater than zero but it's too small to show.
this makes the difference between female mean scores and male mean scores very significant.
-----
207608.7
comparing male mean to female mean distribution when 206 males like shopping.
female mean is .86154 and female standard deviation is .02146
there is a .44 probability that a male mean score of .85833 or lower will occur.
this makes the difference between male mean scores and female mean scores insignificant.
-----
207608.8
comparing female mean to male mean distribution when 206 males like shopping.
male mean is .85833 and male standard deviation is .02266
there is a .44 probability that a female mean score of .86154 or higher will occur.
this makes the difference between female mean scores and male mean scores very significant.
-----
|
|
|