Question 207205This question is from textbook Elementry and Intermediate Algebra
: I need some help please. This type of problem - I just don't get it.
Thomas is going to make an open-top box
by cutting equal squares from the four corners of an
11 inch by 14 inch sheet of cardboard and folding up the
sides. If the area of the base is to be 80 square inches, then
what size square should be cut from each corner?
This question is from textbook Elementry and Intermediate Algebra
Found 2 solutions by RAY100, Theo:
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! Starting with the 11 x 14 sheet,,,and taking a square with sides of "d" away, on all 4 corners, leaves a base of 80 sq inches.
.
(11-2d)(14-2d)=80
154 -22d-28d+4d^2 = 80
4d^2-50d+74=0
2d^2-25d+37=0
.
solve using quadratic formula
.
a=2,,,,b=-25,,,,c=37
.
d=[-(-25)+/-sqrt{(-25)^2 -4(2)(37)}]/2(2)
d=[25+/-sqrt{625-296}]/4
d=[25+/-18.138]/4
d=1.715, 10.785(too big)
.
checking,,,(11-2(1.715))*(14-2(1.715))=(11-3.43)(14-4.43)=80
7.57*10.57=80,,,,ok
.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you need to visualize what's happening and then it's not so bad.
-----
you start off with an 11 x 14 piece of cardboard.
-----
the area of this piece of cardboard is 154 square inches.
-----
the area of the base is going to be 80 square inches.
-----
that will be a piece in the center of the piece of cardboard that will retain the shape of the cardboard.
-----
this means that the length to width ratio will remain the same.
-----
the ratio of the area of the center of the cardboard to the area of the whole cardboard is 80 / 154 = .519480519
-----
in order to retain the same shape, the length and width of the cardboard need to be reduced by the same ratio.
-----
let that ratio be x for now.
-----
if the original dimensions are 11 by 14, then the new dimensions need to be x*11 by x*14 where x is the ratio we are looking for.
-----
this comes out to be x^2 * 11 * 14.
-----
we know the ratio to get from 154 to 80 is .519480419.
-----
this means that x^2 must equal .519480419.
-----
if so, then x must equal 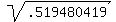 = .72074997 = .72074997
-----
the original length of 14 * .72074997 = 7.928249672
the original width of 11 * .72074997 = 10.09049958
-----
7.928249672 * 10.09049958 = 80 which is the area we are looking for in the center of the cardboard.
-----
the ratio of 14 to 11 is 1.27272727272...
the ratio of 10.09049958 to .72074997 = 1.272727272...
which means we have the area we want and the ratios to the original length to width are the same so the center is in proportion to the whole cardboard.
-----
in my diagram, i have labeled the cardboard ABCD
AB and DC are the widths
AD and BC are the lengths
-----
the center of the cardboard with the same shape is labeled EFHG
EF amd HG are the widths
EH and FG are the lengths
-----
EF is extended to intersect with the lengths of the cardboard at I and J
HG is extended to intersect with the lengths of the cardboard at L and K
-----
EH is extended to intersect with the widths of the cardboard at M and P
FG is extended to intersect with the widths of the cardboard at N and O
-----
This divides the cardboard into 9 rectangles labeled 1 through 9.
The 4 corner rectangles are labeled 1, 2, 3, and 4
The center rectangle is labeled 5
The top and bottom rectangles in the center are labeled 6 and 7
The left and right recgtangles in the center are labeled 8 and 9
-----
areas 1, 2, 3, and 4 are identical
areas 6 and 7 are identical
areas 8 and 9 are identical
-----
lines AB, IJ, LK, and DC are all 11 inches long.
lines AD, MP, NO, and BC are all 14 inches long.
-----
lines MN, EF, HG, and PO are all 7.928249672 inches long
lines IL, EH, FG, and JK are all 10.09049958 inches long
-----
since line IJ is 11 inches long and line EF is 7.928249672 inches long, this means that lines IE and FJ are each equal to (11 - 7.928249672) / 2 = 1.535875164 inches long.
-----
This means that lines AM, IE, LH, DP, NB, FJ, GK, and OC are all each 1.535875164 inches long.
-----
since line MP is 14 inches long and line EH is 10.09049958 inches long. this means that lines ME and HP are each equal to (14 - 10.09049958) / 2 = 1.954750209 inches long.
-----
This means that lines AI, ME, NF, BJ, LD, HP, GO, and KC are all each 1.954750209 inches long.
-----
We now have all the dimensions we need.
-----
The 4 corner rectangles are made up of areas 1, 2, 3, and 4.
-----
area 1 is made up of AM, IE, AI, and ME
area 2 is made up of NB, FJ, NF, and BJ
area 3 is made up of GK, OC, GO, and KC
area 4 is made up of LH, DP, LD, and HP
-----
since all 4 corners share the same dimensions, we can find the area of 1 and that will be the area of each of the others.
-----
rectangle AMEI is area 1.
AM and IE equal 1.535875164 inches long each.
AI and ME equal 1.954750209 inches long each.
area 1 = L * W = 1.535875164 * 1.954750209 = 3.002252298 square inches.
-----
This is enough to answer the question but not enough to verify that our calculations are correct.
-----
the answer you are looking for is:
the dimensions of each of the rectangles in the corners that need to be cut out are:
length = 1.954750209
width = 1.535875164
area = 3.002252298 square inches.
-----
to verify that we segmented the box correctly, we need to get the area of all the rectangles and confirm that the sum of all the areas equals the area of the cardboard.
-----
we have the areas of rectangles 1,2,3,4 and rectangle 5 (this is 80 square inches).
-----
we need the areas of rectangles 6 and 7 next.
length of 6 = 1.954750209
width of 6 = 7.928249672
area of 6 = 15.4977477
area of 7 is the same.
-----
we need the areas of rectangles 8 and 9 next.
length of 8 = 10.09049958
width of 8 = 1.535875164
area of 8 = 15.4977477
area of 9 is the same.
-----
total area of all 9 segments is:
4 * 3.002252298 +
1 * 80 +
2 * 15.4977477 +
2 * 15.4977477 = 154 square inches.
-----
all the dimensions check out.
-----
the answer stands as shown below:
-----
the dimensions of each of the rectangles in the corners that need to be cut out are:
length = 1.954750209
width = 1.535875164
area = 3.002252298 square inches.
-----
the diagram can be found at the following website:
http://theo.x10hosting.com/
-----
click on problem number 207205.
-----
if it's not there when you check, wait one half hour and it will be there.
-----
in that diagram, number 5 is the rectangle that will be the bottom of your open faced box.
rectangles 6,7,8,9 will be folded up.
rectangles 1,2,3,4 will be cut out.
-----
|
|
|