Question 20717: factor completely
x^3+2x^2-3x
Answer by akmb1215(68)   (Show Source):
You can put this solution on YOUR website! The first thing you can do to start factoring this is to look at what each term has in common. In this case, they all have an x. So, you can factor out the x to get 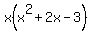 . The x part of the expression is as far down as it can go, so you need to look at the other part (the part in parentheses). You know that you are going to come up with two things, so start out by putting your parentheses...and you know that each is going to have an x in the first part because the first term is x^2, so you can start factoring by writing (x ) (x ) on your paper. Since the last term, 3, is negative, you know that you are going to have one positive and one negative term (because these two numbers multiply to get -3, and the only way to get a negative is to multiply a positive times a negative). So, in the place where you just wrote the x's in parentheses, add a plus to one and a negative to the other to get (x + )(x - ). The final step in factoring a quadratic is to find two numbers that multiply to get the last number (in this case, -3) and that add together to get the second number (in this case, +2). The only two numbers that do that are 1 and 3. Since they have to add to get a positive number, you know that the 3 is the positive and the 1 is the negative. So, your work now looks like (x+3)(x-1). Put this together with the x that you factored out at the very beginning, and you get an answer that looks like this:  .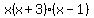
|
|
|
