Question 206914: Solve.
A. x^3-16x>0
B. x^2-5x
Found 2 solutions by RAY100, mickclns:
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! (A) Let x^3 -16x >0 be x^3 -16x =0
.
factoring,,,x(x^2-16) = x(x+4)(x-4) =0,,,
.
or x=0,,,+4,,,,-4
.
To find the inequality, spot these points on a number line ,,,,
.
and then test the intervals.
.
.
_______-4_____________0____________+4____________
.
,,,-5,,,,,,,,,,,,,,,,,,-2,,,,,,,,,,,,,,,,,,,,,,+2,,,,,,,,,,,,,,,,,,,,,+5,,,,,,test points
.
,-45>0,,,,,,,,,,,,,,,,+24>0,,,,,,,,,,,,,,,,,,,-24>0,,,,,,,,,,,,,,,,,,,,45.0,,,,,,x^3-16x>0
.
not true,,,,,,,,,,,,,,, TRUE,,,,,,,,,,,,,,,,,not true,,,,,,,,,,,,,,,TRUE,,,,,,,validity
.
Therefore, -4less than x less than 0,,,,and,,,,x>+4,,,,are valid solutions
.
.
(B) x^2 -5x <= -6
.
x^2 -5x +6 <= 0
.
(x-3)(x-2) <= 0
.
X<= +3, +2
.
again, make a number line and test intervals
.
________+2____________+3
.
,,,0,,,,,,,,,,,,,,,,,,,+2.5,,,,,,,,,,,,,,,,,,,+4,,,,,,,,,,,test points
.
,,0<=-6,,,,,,,,,,,,,,,-6.25<=-6,,,,,,,,,,,,,,,-4<=-6,,,,,,,,,,,evaluation
.
,,not true,,,,,,,,,,true,,,,,,,,,,,,,,,,,,,,,not true,,,,,,,validity
.
also check x= +2,,,-6<=-6,,,,true
.
and x=+3,,,,,-6<= -6,,,,,true
.
Therefore,,,,2<=x<=3,,,,,,valid statement
.
Answer by mickclns(59)   (Show Source): (Show Source):
You can put this solution on YOUR website! A. Let 
Consider the signs of x, x-4, x+4 and y in different parts of the number line.
First we divide the number line at the points where y can be 0 (or y doesn't exist, but that doesn't happen here), that is where x is -4, 0 or 4 (in that order) -- those are the only values of x where y can change sign, from - to + or from + to - (why?). Next, for each of the factors of y, find for what values of x the particular factor can be positive and which negative. For instance, the factor x+4: if we solve the inequality x+4 > 0, we find x > -4. These are the values for which x+4 is positive (that is, >0 ). So look at the row labeled x+4 below. We have a minus where x < -4 and a plus in the three parts of the number line where x > 4. We do a similar thing for x-4 and for x. That takes care of the signs of all three factors, for all values of x. Before going on, make sure you understand everything to this point (for the moment ignore the row labeled y).

Now the reason for laying out this chart of signs. Look at the third column over. This represents all the values of x between 0 and 4. For all of these values, x is +, x-4 is - and x+4 is +. Since y is x(x-4)(x+4) the sign of y is going to be the signs of the factors multiplied, that is, + times - times + which is -, so y is negative between 0 and 4, hence the - sign between 0 and 4 in the row labeled y. Similarly, y is - for all x less than -4, + for all x between -4 and 0, and + for all x greater than 4. So now it is easy to answer the question:
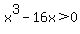 where (remember where (remember  ): either ): either 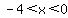 or or 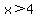 . .
If, instead, say we wanted to find where  , the solution would be: either , the solution would be: either  or or  (look at the same chart of signs). (look at the same chart of signs).
B.
 First add 6 to each side. First add 6 to each side.

Now let  , factor the right side. If you have understood the above it should be easy to apply it to this problem. If it isn't easy, go back over part A and make sure you understand the details, then try B again. , factor the right side. If you have understood the above it should be easy to apply it to this problem. If it isn't easy, go back over part A and make sure you understand the details, then try B again.
|
|
|