|
Question 206027: for the one-to-one function f(x)= 2/x-4
Find the inverse f^-1
Find the domain and range of f
Find the domain and range of f^-1
Answer by mickclns(59)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
To find the inverse function of a function, replace x by y and y (or f(x) ) by x and solve for y
 add 4 to each side add 4 to each side
 change the left side to a fraction and flip both sides change the left side to a fraction and flip both sides
 multiply both sides by 2, then switch sides so y (the inverse of f(x) ) is on the left multiply both sides by 2, then switch sides so y (the inverse of f(x) ) is on the left

Here is a graph of f (red) and its inverse (green, the vertical line at -4 should be ignored, it is not part of either function). Also, graphed is the line y=x ... a function and its inverse are always mirror images of one another across this line, which you can see for the green and the red here.
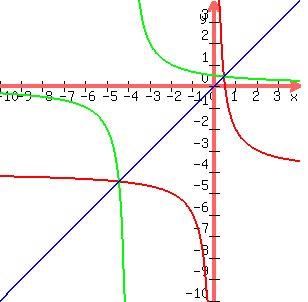
The domain of f is all real numbers except 0 (because x = x-0 is in the denominator makes f(x) undefined).
The range of f is all real numbers except -4 ... for -4 to be the value of y, 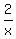 would have to be 0 which means x would have to be infinitely large, but no real number is infinitely large. would have to be 0 which means x would have to be infinitely large, but no real number is infinitely large.
The domain of  is all real numbers except -4 (because x+4 = -4+4 is in the denomiator and makes is all real numbers except -4 (because x+4 = -4+4 is in the denomiator and makes  undefined). undefined).
The range of  is all real numbers except 0 ... for 0 to be the value of y, is all real numbers except 0 ... for 0 to be the value of y, 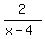 would have to be 0 which means x-4 (and therefore x) would have to be infinitely large, but no real number is infinitely large. would have to be 0 which means x-4 (and therefore x) would have to be infinitely large, but no real number is infinitely large.
|
|
|
| |