Question 205509: Hi,
Pretty sure this is a conditional probability problem or Bayes' Formula problem; can anyone help me figure this out? Thank you so much!
Suppose that a pair of 8-sided dice are rolled (the sides are numbered 1-8).
a) What is the probability that the sum of the dice is 7?
b) What is the probability that the sum of the dice is at least 13?
c) What is the probability that the sum is odd?
Answer by Targetweek(62)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)probability is what you want over all possibilities (kind of vague not technical definition sorry)
-since there are 36 different rolls the denominator is 36
-there are two ways to arrive at that answer, either write out all the different combinations or use the formula

-where n is the number of possible choices and k is the number chosen and a time
-ex. to find the number of different 5-card hands possible, n would be 52 (52 cards in a deck) and k would be 5 (5 cards chosen at a time)
-concerning the two dice is slightly more complicated because there are 16 different choices but if you plug in 16 as n and 2 as k you get 120 combinations which in fact is incorrect. I unfortunately can't explain with a formula how to arrive at that answer but i have a calculator (http://home.att.net/~srschmitt/script_combinations.html) that can list them out for me and i copied them into excel and used some formulas to find the pairs that had both numbers less than or equal to 8, that number was 28 but because the simulation only had 1 of each number, 1-16, it didn't count any of the 8 doubles so i added those in and came up with the 36 different rolls.
-the rolls that equal 7 are...
1 6
2 5
3 4
-so there are 3 possible rolls
-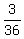 = .0833 or 8.33% = .0833 or 8.33%
b) the bottom is once again 64
-the rolls that are equal to or greater than 13 are...
5 8
6 8
7 8
7 7
7 6
8 8
-there are 5 possible rolls
- or .1666 or 16.66% or .1666 or 16.66%
c)the bottom is once again 64
-the odd sums are 3,5,7,9,11,13,15
-3-
1 2
-5-
1 4
2 3
-7-
1 6
2 5
3 4
-9-
1 8
2 7
3 6
4 5
-11-
3 8
4 7
5 6
-13-
5 8
6 7
-15-
7 8
-so there are 16 different rolls
-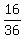 = .4444 or 44.44% = .4444 or 44.44%
|
|
|