Question 205262: Having trouble can not figure this out
for f(x,y)=3x^2y^5+6x^6y^2
compute
fxx(1,-1) =
fxy(2,2)=
fyy(-1,-1) =
thanks so much for help
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Having trouble can not figure this out
for f(x,y)=3x^2y^5+6x^6y^2
compute
 (1,-1) = (1,-1) =
 (2,2) = (2,2) =
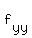 (-1,-1) = (-1,-1) =
thanks so much for help
Find the first partials:
 To find
To find  (x,y), consider y to be
a constant, in the first term (x,y), consider y to be
a constant, in the first term 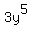 is considered
constant, and in the second term is considered
constant, and in the second term  is considered
constant. If you like, you can rewrite is considered
constant. If you like, you can rewrite  so what
is to be held constant is in parentheses so what
is to be held constant is in parentheses
 Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
 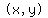 = =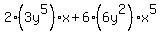 simplifying,
simplifying,
 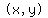 = =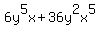 get it in alphabetical order
get it in alphabetical order
 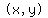 = = ----------------
----------------
 To find
To find  (x,y), consider x to be
a constant, in the first term (x,y), consider x to be
a constant, in the first term  is considered
constant, and in the second term is considered
constant, and in the second term 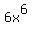 is considered
constant. If you like, you can rewrite is considered
constant. If you like, you can rewrite  so what
is to be held constant is in parentheses so what
is to be held constant is in parentheses
 Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
 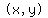 = =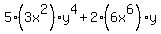 simplifying,
simplifying,
 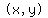 = =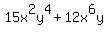 ===============================================
Find the second partial derivative
===============================================
Find the second partial derivative  , which
is the partial derivative with respect to x of
the partial derivative with respect to x.
Start with the partial derivative with respect to x. , which
is the partial derivative with respect to x of
the partial derivative with respect to x.
Start with the partial derivative with respect to x.
 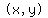 = = To find
To find  (x,y), consider y to be
a constant, in the first term (x,y), consider y to be
a constant, in the first term 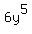 is considered
constant, and in the second term is considered
constant, and in the second term 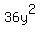 is considered
constant. If you like, you can rewrite is considered
constant. If you like, you can rewrite  so what
is to be held constant is in parentheses so what
is to be held constant is in parentheses
 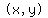 = = Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
 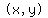 = =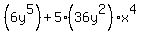 simplifying,
simplifying,
 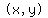 = =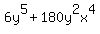 get it in alphabetical order
get it in alphabetical order
 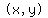 = = And substituting
And substituting
 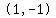 = =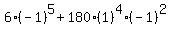
 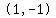 = =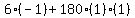
 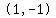 = =
 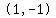 = =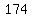 ===============================================
===============================================
Find the second partial derivative
===============================================
===============================================
Find the second partial derivative  , which
is the partial derivative with respect to y of
the partial derivative with respect to x.
Start with the partial derivative with respect to x. , which
is the partial derivative with respect to y of
the partial derivative with respect to x.
Start with the partial derivative with respect to x.
 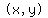 = = To find
To find  (x,y), consider x to be
a constant, in the first term (x,y), consider x to be
a constant, in the first term  is considered
constant, and in the second term is considered
constant, and in the second term 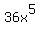 is considered
constant. If you like, you can rewrite is considered
constant. If you like, you can rewrite  so what
is to be held constant is in parentheses so what
is to be held constant is in parentheses
 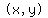 = =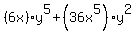 Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
 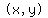 = =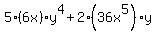 simplifying,
simplifying,
 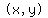 = =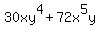 Substituting:
Substituting:
 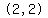 = =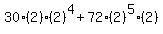
 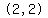 = =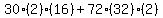
 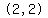 = =
 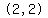 = = ===============================================
===============================================
 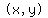 = =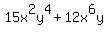 Find the second partial derivative
Find the second partial derivative 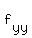 , which
is the partial derivative with respect to y of
the partial derivative with respect to y.
Start with the partial derivative with respect to y. , which
is the partial derivative with respect to y of
the partial derivative with respect to y.
Start with the partial derivative with respect to y.
 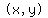 = =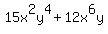 To find
To find 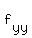 (x,y), consider x to be
a constant, in the first term (x,y), consider x to be
a constant, in the first term  is considered
constant, and in the second term is considered
constant, and in the second term 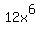 is considered
constant. If you like, you can rewrite is considered
constant. If you like, you can rewrite  so what
is to be held constant is in parentheses so what
is to be held constant is in parentheses
 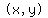 = =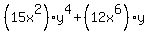 Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
Then we use the ordinary derivative formulas,
considering what is in parentheses as constant:
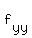 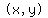 = = simplifying,
simplifying,
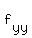 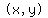 = = Substituting:
Substituting:
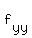 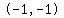 = =
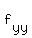 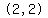 = =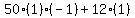
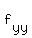 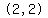 = =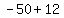
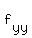 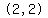 = = Edwin
Edwin
|
|
|