Question 205201: Hi all, I dont quite understand what this questions is asking:
Determine whether the following functions y = xsin3x,  , ,  , ,  are even, odd or none of these. are even, odd or none of these.
Can anyone help me with solving it and explain how to do it please?
Thanks, -Nick.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!  , ,  , , 
The graphs of even functions are symmetrical with respect to the
y-axis. Odd functions are symmetrical with respect to the origin.
There are two ways to show even, odd, or neither. The first way is
graphical. The second way is algebraic. I'll do the graphical way
first:
The graph of 
 It is symmetrical with respect to the y-axis, so it is an even function.
The graph of
It is symmetrical with respect to the y-axis, so it is an even function.
The graph of 
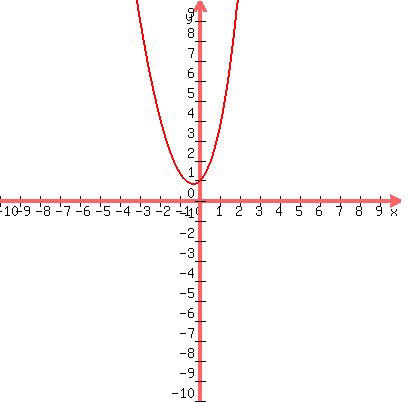 It is not symmetrical with respect to the y-axis or with respect to the
origin so it is neither even nor odd.
The graph of
It is not symmetrical with respect to the y-axis or with respect to the
origin so it is neither even nor odd.
The graph of 
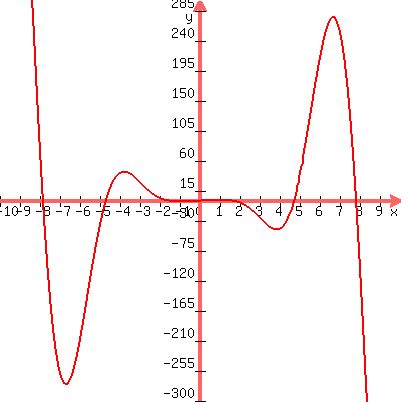 It is symmetrical with respect to the origin, so it is odd.
------------
How to tell algebraically whether the graph will be symmetrical
with the y-axis (even), symmetrical with the origin (odd), or
not symmetrical with respect to either the y-axis or the origin
(neither):
Rules for the algebraic method:
Substitute -x for x and simplify. If you get the same right side
you started with after simplifying, the function is even.
If you get the original right side multiplied by -1, then the
function is odd.
If you get neither, the function is neither even nor odd.
----------------------
It is symmetrical with respect to the origin, so it is odd.
------------
How to tell algebraically whether the graph will be symmetrical
with the y-axis (even), symmetrical with the origin (odd), or
not symmetrical with respect to either the y-axis or the origin
(neither):
Rules for the algebraic method:
Substitute -x for x and simplify. If you get the same right side
you started with after simplifying, the function is even.
If you get the original right side multiplied by -1, then the
function is odd.
If you get neither, the function is neither even nor odd.
----------------------
 replace the x's by (-x)
replace the x's by (-x)

 Use the fact that
Use the fact that 
 Two negatives make a positive
Two negatives make a positive
 This is the same as the original right side so the
function is even.
----------------
This is the same as the original right side so the
function is even.
----------------
 ,
Replace the x's by (-x) ,
Replace the x's by (-x)

 That is neither the same as the original right side,
nor is it the original multiplied by -1,
so it is neither an even nor an odd function.
That is neither the same as the original right side,
nor is it the original multiplied by -1,
so it is neither an even nor an odd function.

 Use the fact that
Use the fact that 
 That is the original right side multiplied by -1, so
the function is odd.
Edwin
That is the original right side multiplied by -1, so
the function is odd.
Edwin
|
|
|