Question 205056: How many terms of the arithmetic sequence 2, 4, 6, 8, ... add up to 60,762? Can anyone help me with the answer and how you solved for it? I am confused and have gotten several different answers trying to do this problem. Thank you
Found 2 solutions by scott8148, MathTherapy:
Answer by scott8148(6628)   (Show Source):
You can put this solution on YOUR website! there is a "canned" formula; but if you look at what's going on, it is pretty straightforward
the difference between consecutive terms in this sequence is 2
the first term is 2
let X be the number of terms it takes to sum to 60762
the value of the nth term is 2n
the sum of the 1st and last terms is 2 + 2X
the sum of the 2nd and next to last terms is 4 + (2X-2) or 2X + 2
the sum of the 3rd and second to last trems is 6 + (2X-4) or 2X + 2
this pattern is consistent
the number of pairs is HALF the number of terms
so the sum of X terms of the sequence is (2X + 2)(X / 2) or X^2 + X
X^2 + X = 60762 ___ X (X + 1) = 60762
so you are looking for two factors of 60762 that are one number apart
___ the values are close to the square root of 60762
___ 246 and 247
246 terms
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website!
The largest number in the sequence is calculated as:  , or:  , which is then calculated using the quadratic equation formula,  , and with a = 1, b = 2, and c = - 243,048
The largest number in the sequence is 492, and that makes the average of the numbers in the sequence 247 (mean or average of the largest and smallest values in the sequence), or, 
Therefore, the number of numbers in the sequence is  ,
calculated as: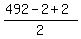 
Check:
Sum of numbers in sequence = average of largest and smallest values, times the number of numbers in the sequence, or, 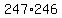 = 60,762. To put it another way, number of numbers in a sequence = Sum of the numbers in the sequence, divided by the average, or mean of the numbers in the sequence, or,
 numbers
|
|
|
