Evaluate

I have this so far
cos^2 theta=(1/2)(1+cos(2theta))
cos((7pi/8))= sqroot((1+cos(7pi/4))/2)
That step is wrong. You must take the NEGATIVE square root,
not the POSITIVE square root, because 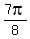 is in
QII (the second quadrant), and the cosine is negative in
the second quadrant. So you should have had a negative
sign in front of the right side:
= sqroot((1+ ((sqroot2)/2))/2)
=sqroot((2+sqroot2)/4)
Those are OK except for the sign. You must recognize
what quadrant you are in whenever you take a square
root, because square roots can be positive or negative.
correct answer:
is in
QII (the second quadrant), and the cosine is negative in
the second quadrant. So you should have had a negative
sign in front of the right side:
= sqroot((1+ ((sqroot2)/2))/2)
=sqroot((2+sqroot2)/4)
Those are OK except for the sign. You must recognize
what quadrant you are in whenever you take a square
root, because square roots can be positive or negative.
correct answer: 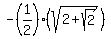 Edwin
Edwin