Question 204859: I have a plate of WHOLE cookies; I gave Jodie half of what was on the plate, plus half of a cookie. I gave Beth half of what was left on the plate, plus half of a cookie; I gave Michelle half of what was left on the plate, plus half of a cookie. There are no cookies left, and I didnít break any in half. How many cookies were on the plate to begin with?
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Well, I tried 7 cookies and that seems to work, and I know that this is not an algebraic answer, but I think that it can be worked out.
Start with 7.
To Jodie, half of 7 is 3.5 plus 0.5 = 4 so there are 3 cookies left.
To Beth, half of 3 is 1.5 pus 0.5 = 2, so now there is 1 cookie left.
To Michelle, half of 1 is 0.5 plus o.5 = 1, no more cookies left and no cookies needed to be broken.
----------------------------------------------------------------------
How did I get 7? Read on!
Let x = the original number of whole cookies on the plate.
To Jodie, you gave:
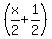 what was left after that can be expressed by: what was left after that can be expressed by:
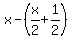 let's call this quantity y, so... let's call this quantity y, so...

To Beth, you gave:
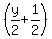 what was left after that can be expressed by: what was left after that can be expressed by:
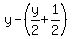 let's call this quantity z, so... let's call this quantity z, so...

To Michelle, you gave:
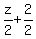 what was left after that can be xepressed by: what was left after that can be xepressed by:
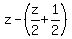 ...and, because there were no cookies left, we'll call this zero, so... ...and, because there were no cookies left, we'll call this zero, so...
 Now we can solve this for z: First simplify it. Now we can solve this for z: First simplify it.
 Multiply both sides by 2. Multiply both sides by 2.
 Add 1 to both sides. Add 1 to both sides.
 Now we know z, we can solve for y. Now we know z, we can solve for y.



 Finally, we can solve for x, the original number of cookies. Finally, we can solve for x, the original number of cookies.




|
|
|