SOLUTION: Six people are selected at random. What is the probability that none of the people in this group were born in the same month? (I need to know how to set this up. thanks!)

                         NUMBER OF SUCCESSFUL WAYS
PROBABILITY = -------------------------------------------------
               TOTAL NUMBER OF WAYS, SUCCESSFUL OR UNSUCCESSFUL


To be successful we must do this:

1. assign the first person a birthday month (12 ways)
   then 
2. assign the second a different birthday month (11 ways)
   then
3. assign the third a birthday month different from the other two. (10 ways)
   then 
4. assign the fourth a different birthday month different from the other three. (9 ways)
   then 
5. assign the fifth a birthday month different from the other four(8 ways)
   then 
6. assign the sixth a different birthday month different from the other five(7 ways)
   
So the numerator of the probablity is 12*11*10*9*8*7

---

To get the number of possibilities, successful or unsuccessful,

1. assign the first any birthday month (12 ways)
   then 
2. assign the second any birthday month (12 ways)
   then
3. assign the third any birthday month. (12 ways)
   then 
4. assign the fourth any birthday month. (12 ways)
   then 
5. assign the fifth any birthday month. (12 ways)
   then 
6. assign the sixth any birthday month. (12 ways)
   
So the denominator of the probablity is 12*12*12*12*12*12

The desired probability is

  12*11*10*9*8*7        665280
-----------------  =  ----------
12*12*12*12*12*12       2985984
 
 That reduces by dividing by 1720 to 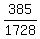  or about 0.2228

Edwin