Question 204250: How do you complete this function equation f(x)=-2x^2+8x-5. I need to find the vertex h,k , compute h and k and graph the quadratic equation. Plus find the max value of f where it occurs.
I started the equation and found h.
a=-2 b=8 c=-5, so using the ormula -b/2a I got -8/2(-2) which gave me -8/-4 which gave me 2. h=2. Where do I go from here?
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! How do you complete this function equation f(x)=-2x^2+8x-5. I need to find the vertex h,k , compute h and k and graph the quadratic equation. Plus find the max value of f where it occurs.
I started the equation and found h.
a=-2 b=8 c=-5, so using the ormula -b/2a I got -8/2(-2) which gave me -8/-4 which gave me 2. h=2. Where do I go from here?
.
What you found:
-b/2a = 2
is the "axis of symmetry"
.
To find 'k', simply plug 2 back into the equation and solve:
f(x)=-2x^2+8x-5
f(2)=-2(2)^2+8(2)-5
f(x)=-8+16-5
f(x)=3
.
So, (h,k) = (2,3) vertex
.
To plot, looking at the 'a' coefficient (-2), we KNOW it is a parabola that opens downward. Use the "vertex" above and find two additional points to plot. The two additional points could be where the parabola crosses the x-axis:
0=-2x^2+8x-5
.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=24 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 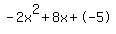 can be factored: can be factored:

Again, the answer is: 0.775255128608411, 3.22474487139159.
Here's your graph:
 |
|
|
|