Question 204141: Could anyone help me with this. I am not sure how to do it. I really need your help.
Do exponential functions only model phenomena that grow, or can they also model phenomena that decay? Explain what is different in the form of the function in each case.
Answer by Earlsdon(6294)   (Show Source):
You can put this solution on YOUR website! Exponential functions model both phenomena that grow and phenomena that decay.
The general form for the exponential function is:
 b is called the base.
For growth phenomena, the base,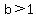 
For decay phenomena, the base,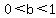 
A typical example of exponential grow is the increase in money deposited in savings account.
For example, if you deposited $500 at 5% interest per year, how much would you have at the end of 4 years?
The formula is:
 where:
A = the amount you would have at the end of 4 years..
P = the principal (amount invested).
r = the rate of interest, in decimal form.
t = the length of time deposited, in years.
In our example, P = $500, r = 0.05, and t = 4 years.
 Use your calculator to get the approximate value of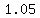 
You would have $607.75 in 4 years.
----------------------------------
A typical example of exponential decay is the decrease of radio-active material (radio-active decay) after a length of time.
The term "half-life" is used to indicate the length of time it takes for radio-active material to lose half of its mass.
For example:
The half-life of an isotope of thorium, thorium-234, is 25 days.
If you started with 50 grams of thorium- 234, how much would be left after 100 days?
Since the amount of thorium-234 decreases 50% every 25 days, the exponential function for the decay is:
 where t = the number of half-lives that have elapsed. Notice that the base (b = 0.5) is less than 1.
 half-lives.
 grams.
|
|
|
