Question 203931: could you guide me about this? I dont have any idea to solve this kind of exercises and I don't know what do I have to do.Thanks.
Use the fundamental identities to find all of the trigonometric ratios if the variable satisfies the given conditions.
a) sin x=12/13 and cos x<0
b)cos x =-4/3 , sinx>0
c)tan x = -24/7 , sinx>0
d)tan x = 4/3 , sinx>0
e)cot x= 4 , sinx>0
f)cos x=3/5
p.s: I've written all cause I've thought maybe there are different points.
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Use the fundamental identities to find all of the trigonometric ratios if the variable satisfies the given conditions.
a) sin x=12/13 and cos x<0
cos^2 = 1 - sin^2
cos^2 = 1 - 144/169 = 25/169
cos = 5/13
x = arccos(5/13) = arccos(-5/13)
x = ~ -67.38º
------------------
b)cos x =-4/3 , sinx>0
c)tan x = -24/7 , sinx>0
d)tan x = 4/3 , sinx>0
e)cot x= 4 , sinx>0
f)cos x=3/5
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Edwin's solution:
a)  and and 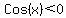 The sine is positive and the cosine is negative
only in quadrant II
To find
The sine is positive and the cosine is negative
only in quadrant II
To find 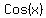 : :
 <-- fundamental identity to use <-- fundamental identity to use





 But we are given that
But we are given that 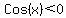 so we choose the negative answer for
so we choose the negative answer for 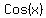 ,
therefore: ,
therefore:

 ------------------
To find
------------------
To find 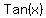 : :
 <-- fundamental identity to use. <-- fundamental identity to use.
 ------------------
To find
------------------
To find 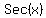
 <--- fundamental identity to use <--- fundamental identity to use
 -------------------
To find
-------------------
To find 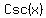
 <--- fundamental identity to use <--- fundamental identity to use
 ==================================================
b)
==================================================
b) , , 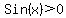 Sorry this is a mistake because
Sorry this is a mistake because  and
cosines are always between and
cosines are always between  and and  .
So if you didn't copy it wrong, then there
is no solution!
=================================================
c) .
So if you didn't copy it wrong, then there
is no solution!
=================================================
c)  , , 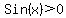 The tangent is negative and the sine is positive
only in quadrant II
To find
The tangent is negative and the sine is positive
only in quadrant II
To find 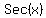 : :
 <-- fundamental identity to use <-- fundamental identity to use





 But since this is in Quadrant II, the secant, which
is the reciprocal of the cosine, is negative, we choose
the negative answer for
But since this is in Quadrant II, the secant, which
is the reciprocal of the cosine, is negative, we choose
the negative answer for 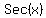 , therefore: , therefore:

 ------------------
To find
------------------
To find 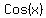 : :
 <-- fundamental identity to use. <-- fundamental identity to use.

 ------------------
To find
------------------
To find 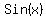 : :
 <-- fundamental identity to use <-- fundamental identity to use





 But we are given that
But we are given that 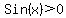 so we choose the positive answer for
so we choose the positive answer for 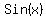 ,
therefore: ,
therefore:

 -------------------
To find
-------------------
To find 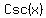
 <--- fundamental identity to use <--- fundamental identity to use
 -------------------
To find
-------------------
To find 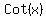 : :
 <-- fundamental identity to use. <-- fundamental identity to use.
 ==================================================
d)
==================================================
d)  , , 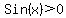 The tangent is positive and the sine is positive
only in quadrant I, so all trigonometric ratios are
positive:
To find
The tangent is positive and the sine is positive
only in quadrant I, so all trigonometric ratios are
positive:
To find 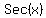 : :
 <-- fundamental identity to use <-- fundamental identity to use





 But since this is in Quadrant I, all trig rations are
positive therefore:
But since this is in Quadrant I, all trig rations are
positive therefore:

 ------------------
To find
------------------
To find 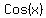 : :
 <-- fundamental identity to use. <-- fundamental identity to use.

 ------------------
To find
------------------
To find 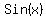 : :
 <-- fundamental identity to use <-- fundamental identity to use





 But we are given that
But we are given that 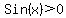 so we choose the positive answer for
so we choose the positive answer for 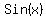 ,
therefore: ,
therefore:

 -------------------
To find
-------------------
To find 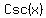
 <--- fundamental identity to use <--- fundamental identity to use
 -------------------
To find
-------------------
To find 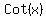 : :
 <-- fundamental identity to use. <-- fundamental identity to use.
 -------------------------------
e)
-------------------------------
e)  , sinx>0
The cotangent is positive and the sine is positive
only in quadrant I, so all trigonometric ratios are
positive:
To find , sinx>0
The cotangent is positive and the sine is positive
only in quadrant I, so all trigonometric ratios are
positive:
To find 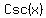 : :
 <-- fundamental identity to use <-- fundamental identity to use




 But since this is in Quadrant I, all trig ratios are
positive therefore:
But since this is in Quadrant I, all trig ratios are
positive therefore:
 ------------------
To find
------------------
To find 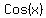 : :
 <-- fundamental identity to use. <-- fundamental identity to use.

 ------------------
To find
------------------
To find 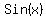 : :
 <-- fundamental identity to use <-- fundamental identity to use






 But we are given that
But we are given that 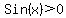 so we choose the positive answer for
so we choose the positive answer for 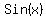 ,
therefore: ,
therefore:

 -------------------
To find
-------------------
To find 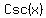
 <--- fundamental identity to use <--- fundamental identity to use
 -------------------
To find
-------------------
To find 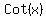 : :
 <-- fundamental identity to use. <-- fundamental identity to use.
 =====================================================
f)
=====================================================
f)  You didn't give enough information, as you need to be
given that another trig ratio is >0 or <0.
Edwin
You didn't give enough information, as you need to be
given that another trig ratio is >0 or <0.
Edwin
|
|
|