Question 203835: Write the slope-intercept equation of the line that is parallel to, -3x-5y=6 and has the same y-intercept as the graph of, 2x+y=-4
Answer by PRMath(133)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write the slope-intercept equation of the line that is parallel to: -3x-5y=6 and has the same y-intercept as the graph of: 2x+y=-4
Ok, first we have to write a line that is parallel to -3x - 5y = 6. What you have to know is that parallel lines have the SAME slope. So, we just have to find the slope of this line: -3x - 5y = 6. How do we do that? Let's solve this equation for y and in doing so, we'll put the equation in slope/intercept form. The slope intercept form is y = mx + b. In this form, the "m" is the slope. So, let's go.......
First we solve for y:
-3x - 5y = 6 (add 3x to both sides)
-5y = 3x + 6 (now divide both sides by -5 to isolate the y)

y = 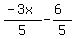
Now can you see that your slope for the line is 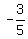 ? Therefore, our next line that we create has to have this for a slope if the two lines are going to end up being parallel. ? Therefore, our next line that we create has to have this for a slope if the two lines are going to end up being parallel.
Now the next part of your problem says: the line must have the same y-intercept as the graph of, 2x + y = -4. Hmmmm... What is the y intercept of this line? Here's something for you to know:
To find the y intercept, solve for y by making x = 0.
To find the x intercept, solve for x by making y = 0.
SO in our equation: 2x + y = -4
We just need to solve for y by making x = 0. Let's try it:
2x + y = -4 (original equation)
2(0) + y = -4
0 + y = -4
y = -4
SO we know that when x = 0, then y = -4. Our y intercept is -4.
Now what do we want? We want a line in the slope/intercept form (y = mx + b) and remember, that "m" is the slope. What you also have to know is that "b" is the y intercept. We want this new equation of a line to be parallel to the first line -3x - 5y = 6, which means the 2nd line must have (as we know from above) a slope of 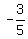 . .
SO let's plug in our info to the equation of:
y = mx + b
y = 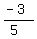 x - 4 x - 4
Do you see how we "plugged in" the value for m, which was 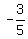 as well as the value for "b" which was -4? as well as the value for "b" which was -4?
Does that make sense for you? I hope so. :-)
|
|
|