Question 203335: If 1 ≤ a ≤ 10 and 1 ≤ b ≤ 36, for how many ordered pairs of integers (a, b) is
square root ( a + square root b) an integer?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! In order for 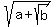 to be an integer, to be an integer, 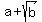 must be a perfect square. And for must be a perfect square. And for 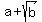 to be a perfect square, to be a perfect square, 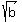 must be an integer. And finally, in order for must be an integer. And finally, in order for 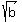 to be an integer, b must be a perfect square. to be an integer, b must be a perfect square.
So we'll start by checking possible values for "b": perfect squares between 1 and 36 (inclusive). And we will then see if we can find an "a", between 1 and 10 (inclusive) which makes the rest of the expression work out as desired.- "b" is 1
- "a" = 3 works:
 - "a" = 8 works:

- "b" = 4
- "a" = 2 works:
 "a" = 7 works 
"b" = 9- "a" = 1 works:
 - "a" = 6 works:

"b" = 16- "a" = 5 works

"b" = 25- "a" = 4 works

"b" = 36- "a" = 3 works

So the solutions as ordered pairs:
(3, 1)
(8, 1)
(2, 4)
(7, 4)
(1, 9)
(6, 9)
(5, 16)
(4, 25)
(3, 26)
|
|
|