SOLUTION: (4X^3+4) DIVIDED BY (X-1)

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: (4X^3+4) DIVIDED BY (X-1)      Log On


   

Question 203126This question is from textbook I can Learn Algebra Vol. 1
: (4X^3+4) DIVIDED BY (X-1) This question is from textbook I can Learn Algebra Vol. 1

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!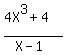
%284X%5E3%2B4%29%2F%28X-1%29
This is an expression and the only thing you can do with an expression is simplify it. Some (but not necessarily all) of the things to do when simplifying are (in no particular order):
  • Perform all possible operations, using the order of operations (aka PEMDAS)
  • Reduce fractions by canceling common factors, if any
  • Simplifying square (and other roots), if possible
  • Make substitutions using trigonometric identities to simplify
  • Replace logarithms with simpler expressions, if possible

In your expression, only the first two could apply since you have no roots, trig functions or logarithms. As the numerator and denominator stand the addition and the subtraction cannot be performed because they are not like terms. There is no multiplication. And before we try to divide let's try to reduce the fraction first. (If it reduces, then the division will be easier.)

To reduce any fraction we need to find the common factors first so we can see if there are common factors which can be canceled. And whenever you factor, always start with the Greatest Common Factor (GCF). The numerator has a GCF of 4 and the denominator has a GCF of 1 (which we do not usually factor out unless we need it). So after factoring out the GCF of the numerator we get:
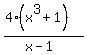
%284%28x%5E3+%2B+1%29%29%2F%28x-1%29
After you factor out the GCF there are a variety of factoring techniques which one can try to use to see if the expression factors further: patterns, grouping, trinomial factoring, etc. The 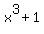x%5E3+%2B+1 factor fits the a%5E3+%2B+b%5E3+=+%28a+%2B+b%29%28a%5E2+-+ab+%2B+b%5E2%29 pattern (with a = x and b = 1). Using this pattern to factor we now get:
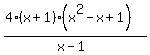
%284%28x+%2B+1%29%28x%5E2+-+x+%2B+1%29%29%2F%28x-1%29
At this point we find that no more factoring can be done. (Always remember to keep factoring until no more can be done.) We also see that there are no common factors. So nothing cancels which means the fraction will not reduce.

(But I have to wonder if the denominator was supposed to be (x+1) instead of (x-1) or if the numerator was supposed to be 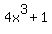4x%5E3+-+1 instead of 4x%5E3+%2B+1. If so then we would have a common factor and the entire denominator cancels out. This would eliminate the entire fraction, simplifying the expression dramatically.)

So if the problem you posted is correct, then the fraction will not reduce. All we can do is divide out the fraction. This can be done with long division or Synthetic Division. The following is long division:
     4x^2  +  4x     +  4
     ____________________________
x-1 /4x^3  +  0x^2   +  0x   +  4
     4x^3  + -4x^2
     -------------
              4x^2   +  0x
              4x^2   + -4x
              ------------
                        4x   +  4
                        4x   + -4
                        ---------
                                8

So %284x%5E3+%2B+4%29%2F%28x-1%29+=+4x%5E2+%2B+4x+%2B+4+%2B+8%2F%28x-1%29. But it is not clear that the right side is "simpler" than the left side. So the answer is either the right side or "The expression does not simplify", depending on which side is considered "simpler".