Question 203108: Factor the Polynomial 4x^3-28x^2+49x. First find the GCF of the terms 4x^3, 28x^2, and 49x, and factor it out of the polynomial 4x^3-28x^2+49x.Then use the appropriate pattern for factoring the remaining expression.
Thanks i really appreciates this.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
Factor out the GCF:
The only factor common to all three terms is x. So the GCF is x. Factoring this out we get:
Next we will try to factor  using patterns. The patterns which are most often taught are:- Difference of squares:
 - Difference of cubes:
 - Sum of cubes:
 - Perfect square trinomials:
Since the first three patterns factor binomials (two-term expressions) and since we have a trinomial (three-term expression), we will not be able to use the first three patterns. And since the fourth pattern has a "+" in front of the middle term and we have a "-", that pattern is out, too. The only possible pattern for is the last one:  .
To see if our expression fits the pattern:- The first term in the pattern,
 means that the first term in our trinomial must be a perfect square. Since  it is a perfect square. It is "2x squared". So our "a" is 2x. - The last term in the pattern is
 , a perfect square. So our last term has to be a perfect square (or we will not be able to use this pattern). Our last term, 49, is 7 squared. So it is a perfect square and our "b" is 7. - Last of all we need to see if our middle term fits the pattern's middle term which is 2ab. Since our "a" is 2x and our "b" is 7, 2ab = 2*(2x)*7 = 28x, our middle term!
Since all three terms of our trinomial fit the pattern of  with "a" = 2x and "b" = 7, our trinomial will factor according to this pattern:
Now our complete expression is:
Remember, factoring is like reducing fractions: You keep going it until you can't go it any further. However, since 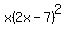 will not factor any further, we are finished.
|
|
|
