|
Question 202899: Which one of the following is true about the graph of f(x)=2f^x-12+30? (1)The range is (-infinity,infinity). (2) The domain is bracket0,infinity). (3) There is a vertical asymptote at x=12. (4)There is a horizontal asymptote at y=30. Thank-you for your help, very much appriciated.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x) = 2f^x-12+30
Is this:  ? If so: ? If so:- It is very unusual (and confusing) for "f" to be used both as the name of the function and as a variable!
- The function "f" is not a function of just "x". It is a function of both "x" and the variable "f"! It would be f(x, f).
- Please correct the problem and repost it. Please use more parentheses to ensure clarity.
If the second "f" was a typo the function is:

then we answer the problem:
(1)The range is (-infinity,infinity).
The range is the set of possible value for the function. So we need to figure out the possible values for 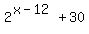 . If we understand exponents then we will realize that: . If we understand exponents then we will realize that:- 2 to any power can never be zero. Therefore
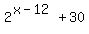 never have a value of 30 never have a value of 30 - 2 to any power can never be negative. Therefore
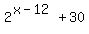 can never be less than 30. can never be less than 30. - 2 to a very large negative power will be a very tiny fraction which is very close to zero in value. Therefore
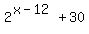 can be very, very close to (but never equal to) 30 when x is a large negative number. can be very, very close to (but never equal to) 30 when x is a large negative number. - 2 to a power will become an infinitely large positive number as x gets to be an infinitely large positive number.
Therefore the range is (30, infinity).
(2) The domain is [0,infinity).
The domain is the set of possible x-values. The x in f(x) is found only in the exponent of 2. Since exponents can be any number and since there are no other reasons to exclude x-values (like zeros in denominators, negatives in a square roots, zeros or negatives in logarithms, etc.) the domain of f(x) is all Real numbers: (-infinity, infinity)
(3) There is a vertical asymptote at x=12.
If we had a vertical asymptote at x=12 then 12 would be excluded from the domain. But 12 is in the domain.
(4)There is a horizontal asymptote at y=30.
Horizontal asymptotes occur when the function values approach a certain number when x-values become very large positive or negative numbers. When x is a very large positive number, 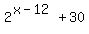 becomes a very large positive number. The larger x gets, the larger becomes a very large positive number. The larger x gets, the larger 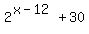 gets. gets.
But when x is a very large negative number, 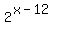 becomes a very tiny fraction and becomes a very tiny fraction and 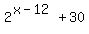 becomes a number just a tiny bit above 30. The more negative x gets, the tinier the fraction and the closer becomes a number just a tiny bit above 30. The more negative x gets, the tinier the fraction and the closer 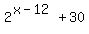 gets to 30. So on the left side of the graph of gets to 30. So on the left side of the graph of 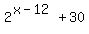 (where x gets more and more negative, the graph will get closer and closer to y = 30. We do have a horizontal asymptote at y = 30. (where x gets more and more negative, the graph will get closer and closer to y = 30. We do have a horizontal asymptote at y = 30.
|
|
|
| |