A survey of 900 Americans found that 680 had confidence in the economy. If 80% of the women and 70% of the men surveyed expressed confidence in the economy then how many men were surveyed?
Let W = the number of women
Let M = the number of men
>>...A survey of 900 Americans...<<
(number of women) + (number of men) = (980 people)
W + M = 980
>>...680 had confidence in the economy...<<
>>...80% of the women and 70% of the men...expressed confidence...<<
(80% of the number of women) + (70% of the number of men) = (680 people)
.80W + .70M = 680
So we have the system:
 Multiply the second equation through by 10 to remove decimals:
Multiply the second equation through by 10 to remove decimals:
 Solve the first equation for one of the letters, I'll pick M.
Solve the first equation for one of the letters, I'll pick M.
 subtract W from both sides
subtract W from both sides
 Substitute
Substitute 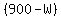 for
for  in
in



 Add -6300 to both sides:
Add -6300 to both sides:
 So there were 500 women. Substituting 500 for W in
So there were 500 women. Substituting 500 for W in


 So there were 400 men.
Edwin
So there were 400 men.
Edwin