|
Question 202690: I am having trouble with finding the domain for expressions like f(t)=log(t-5), g(x)=5e^x, g(x)=ln(x+4) and g(t)= 5^t. The concept eludes me, can anyone help with how to go about solving these??
E.T.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the domain is the possible values that x can take.
the range is the possible values that y can take.
domain is possible values that x can take.
range is the possible values that y can take.
-----
your first problem:
f(t) = log(t-5)
you cannot take the log of any number that is 0 or less than 0.
your equation is y = log(t-5)
your domain is (t-5)
your range is log(t-5)
in this case (t-5) must be greater than zero which means that t must be > 5.
-----
your second problem is g(x) = ln(x+4).
same deal.
you cannot take the natural log of any number if it is 0 or less.
your equation is y = ln(x+4)
your domain is x+4 and your range is y which is ln(x+4)
your domain has to be > 0, so x+4 have to be > 0 which can only be if x > -4.
your domain is x > -4
-----
your third problem is g(x) = 5e^x
this is the same as y = 5e^x
x is your domain.
5e^x is your range.
in this particular case, there does not appear to be any restrictions to the value of x.
x can be any real number (negative, 0, or positive).
-----
your fourth problem is g(t) = 5^t.
this is the same as y = 5^t.
there do not appear to be any restrictions to the value of t, which is your domain.
t is your domain.
5^t is your range.
t can be any real number (negative, 0, or positive).
-----
exponents and logs are inverse relationships to each other.
if it wasn't for exponents, logarithms would not exist.
the rules are:
y = b^x if and only if x = 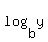
if y = b^x, the inverse function is y = 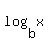
while x in the exponent equation can be any real number, x in the logarithm equation has to be > 0.
-----
in any equation, if y = f(x), x is the domain, and f(x) is the range.
-----
I hope this answers your quesation.
If it doesn't, send me an email with the specific area of discomfort, and I'll try to ease it for you.
|
|
|
| |