Question 202611: Take any number (except for 1). Square that number and then subtract one. Divide by one less than your original number. Now subtract your original number. You reached 1 for an answer, didn’t you? How does this number game work? (Hint: Redo the number game using a variable instead of an actual number and rewrite the problem as one rational expression). How did the number game use the skill of simplifying rational expressions? Create your own number game using the rules of algebra and post it for your classmates to solve.
I have done everything in this question except for a number game. I understand rational expressions, I just do not understand how I can create a game using the rules of algebra.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Take any number (except for 1).
Let's call our number "x"
Square that number
and then subtract one
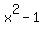
Divide by one less than your original number.
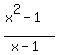
(Note that this is why the problem says we can't use 1. If we use 1, then (x-1) would be zero and we can never allow a denominator to be 0!)
Now subtract your original number
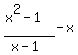
Now let's simplify this expression. When you have fractions, reducing them often make the rest of the problem easier. So before we try to subtract x from the fraction, let's try to reduce the fraction first. You reduce fractions by canceling common factors. So we need to factor the numerator and denominator to see if there are common factors to cancel. The numerator, 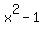is a difference of squares so it will factor according to the  pattern. (The denominator will not factor other than to factor out a 1.)
So our expression with the factored fraction looks like:
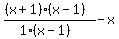
We can see that the (x-1)'s in the fraction will cancel. In fact the fraction has "disappeared". Now we have:
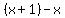
Simplifying this we see that the x's cancel leaving just 1!
To create your own number game, the key, I believe, is to work backwards!- Start by deciding what the final answer will be
- Now change the answer by performing actions which do not change the value:
- Adding zero. But instead of adding 0, we add "strange-looking" zeros like
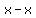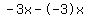 ,  ,  , etc. - Multiplying by 1. Again we will not multiply by 1 but by "strange-looking" ones like
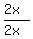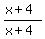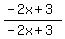 ,  ,  , etc. - Use the Commutative and Associative properties to change the order and/or grouping of terms
If you read the solution of the number game we solved above backwards, note that zeros get added, parts of expressions get multiplied by ones, and the order and grouping of terms are changed. - As you make the changes described above, your expression, which started as a single number, becomes more and more complex.
- At some point stop making your expression more complex. Now you just explain, in words, how to build the expression you have created. And, of course, you will explain that what the answer should be.
|
|
|
