SOLUTION: hyperbola {{{9(x-1)^2/16 - (y+1)^2/9 =1}}} find: center, foci, vertices, asymptotes I can't figure out how to get rid of first 9 elipse given: vertices(-2,4);(-2,-2) passin

To get rid of the 9:
 
First write the first term 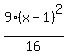 as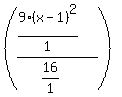 
 
Then multiply it by the fraction  which just 
equals .  So we have this:
 

 
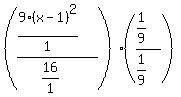Then we can cancel the 9's in the top:
 

 
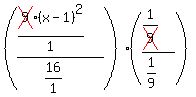and we end up with
 

 
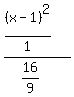And we can dispense with the 1 denominator in the
top:
 

 
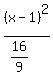A shortcut is to do it all in one step by learning
to move the 9 from the top down under what's on the bottom.
 
So, in this:
 

 
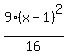Just move the 9 down under the 16 on the bottom
and in just one step you have this:
 

 
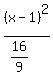and you don't have to go through all that I did above every time.
I just did that to show why it works to just move a factor from
the numerator down underneath the denominator, causing the
denominator to become a fraction.
 
--------------------------- 
 
Anyway the equation is now:
 

 
Compare that to
 

 
and , , 
 so 
, so 
-----------------------------------------------
 
I won't finish that one for you.  However I'll do one similar, 
that is the same kind of hyperbola but the numbers are different.







 
, , 
 
, so 
 
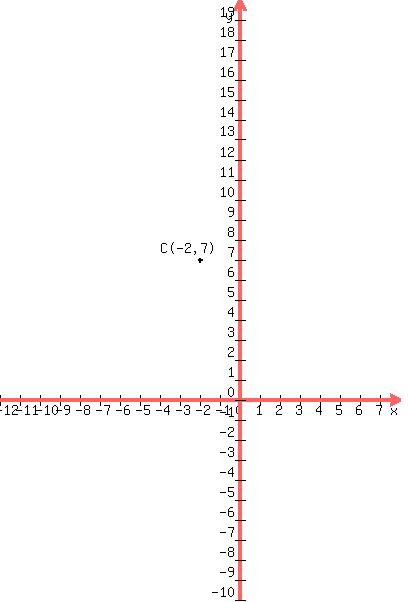
, so 
 
The center (h,k) = (-2,7)
 
We start out plotting the center C(h,k) = C(-2,7)
 

 
Next we draw the left semi-transverse axis,
which is a segment a=5 units long horizontally 
left from the center.  This semi-transverse
axis ends up at one of the two vertices (-7,7).
We'll call it V1(-7,7):
 

 
Next we draw the right semi-transverse axis,
which is a segment a=5 units long horizontally 
right from the center. This other semi-transverse
axis ends up at the other vertex (3,7).
We'll call it V2(3,7):
 

 
That's the whole transverse ("trans"="across",
"verse"="vertices", the line going across from
one vertex to the other. It is 2a in length,
so the length of the transverse axis is 2a=2(5)=10
 
Next we draw the upper semi-conjugate axis,
which is a segment b=8 units long verically 
upward from the center.  This semi-conjugate
axis ends up at (-2,15).
 

 
Next we draw the lower semi-conjugate axis,
which is a segment b=8 units long verically 
downward from the center.  This semi-conjugate
axis ends up at (-2,-1). 
 

 
That's the complete conjugate axis. It is 2b in length,
so the length of the transverse axis is 2b=2(8)=16
 
Next we draw the defining rectangle which has the
ends of the transverse and conjugate axes as midpoints
of its sides:
 

 
Next we draw and extend the two diagonals of this defining
rectangle:
 

 
Now we can sketch in the hyperbola:
 


The foci are points inside the hyperbola, which are the distance c
from the center, where c is calculated by

  (just like the Pythagorean theorem, from whence
it comes):







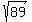So the two foci are  units 
right and left of the center, which is
(h,k) = (-2,7)

Therefore the foci are:

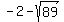(,7) and (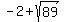,7) 

They are approximately the points:

(-11.4,7) and (7.4,7).  I won't bother plotting
them.

All that's left to do is find the equations of the two asymptotes.
Their slopes are ± or ±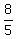
 
The asymptote that has slope  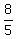goes through the center
C(-2,7), so its equation is found using the point-slope
formula:
 



Multiply through by 5



 
The asymptote that has slope  goes through the center
C(-2,7), so its equation is found using the point-slope
formula:
 



Multiply through by 5



 

----------------------------------------------- 


elipse

given: vertices(-2,4);(-2,-2) passing through (0,1)

find the equation

I get the answers but my signs are wrong or I get 1/16th instead of 16 


Plot the two vertices:



We can see that this is a vertical ellipse, that is, one that looks like
the number zero "0" and not like an egg sitting on a table, so its equation
is



The center of an ellipse is the midpoint of the line joining
the vertices.  We can therefore easily calculate, or just look 
and see that the midpoint between those vertices is the point
(-2,1), so we plot that point too:



So that is the center of the ellipse, so now we know that

 and .

We also know that  because  is the semi-major axis
which is the distance from the center to either vertex.

Now we are given that the ellipse goes through the point (0,1).
So let's plot that.



As we can now see, that is a very special point, for since 
the point (0,1) has the same y-coordinate as the center (-2,1), that
means that (0,1) is a "minor vertex" or an end of the semi-minor
axis. Let's sketch in the ellipse:



Since  represents the length of the semi-minor axis,
and since there are 2 units between the center (-2,1) and (0,1), that
tells us that 

So we now have , ,  and .

So we plug those into:



and get



or



(Hmmm! I didn't see anything about either 16 or 1/16th)

Edwin