Question 202488: Can someone PLEASE help me with these? Thank You. :)
1) A person is wearing a bracelet with 11 settings around the bracelet. How many different ways can 11 birthstones be arranged around the bracelet? Leave the answer in factorial form.
2) How many subsets of four elements each exist in a set of seven elements?
3) How many different groups of 35 cars can be formed from 40 cars?
4) How many different ways can an executive committee of nine people sit at a round table?
5) What is the probability of not drawing a green marble from a jar containing 7 red, 4 green, 3 white, and 9 blue marbles?
6) A compound experiment consists of drawing at random twice without replacing from a jar with 3 red, 3 white, and 2 black marbles. What is the probability of getting first a red and then a black marble?
Thanks again,
~Sarah
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! permutations are an ordered set. each set can contain the same elements as another set only in a different order.
the formula for permutations is:
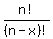
-----
combinations are an unordered set. each set cannot contain the same elements as another set regardless of the order.
the formula for combinations is:
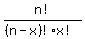
-----
a simple example:
letters abc.
sets of 2 letters
permutations would be: ab, ba, ac, ca, bc, cb.
formula for permutations would be  = 6 = 6
note that 1! was the result of (3-2)! which = 1!.
combinations would be: ab, ac, bc
formula for combinations would be 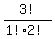 = 3 = 3
-----
your problems:
-----
1) A person is wearing a bracelet with 11 settings around the bracelet. How many different ways can 11 birthstones be arranged around the bracelet? Leave the answer in factorial form.
we're looking for permutations here.
the formula should be how many permutations of 11 can you get out of a set of 11.
the formula should be:
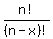
where:
n = 11 = set you are drawing from.
x = 11 = set you want to create.
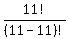 = = 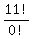 = = 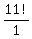 = =  . .
please note that 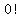 = 1. = 1.
this may be counter-intuitive but it is correct. if you want to see a decent explanation, go to this website and look at the best answer to the question.
-----
http://answers.yahoo.com/question/index;_ylt=AsdGQIzGmbF_exSCD_gWWxYjzKIX;_ylv=3?qid=20060811004831AAT49h4
-----
anyway, back to your problem.
 = 11*10*9*8*7*6*5*4*3*2*1 = 39,916,800 possible ways the birthstones can be arranged on the necklace. = 11*10*9*8*7*6*5*4*3*2*1 = 39,916,800 possible ways the birthstones can be arranged on the necklace.
-----
if it was 2 beads they could be arranged 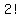 ways = 2*1 = 2 ways ways = 2*1 = 2 ways
if it was 3 beads they could be arranged 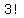 ways = 3*2*1 = 6 ways ways = 3*2*1 = 6 ways
if it was 4 beads they could be arranged 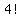 ways = 4*3*2*1 = 24 ways ways = 4*3*2*1 = 24 ways
you can see as the number of beads gets larger, the possible permutations (these are permutations because they contain the same beads only in a different order) becomes much larger.
-----
2) How many subsets of four elements each exist in a set of seven elements?
looks like they want combinations here since order is not important.
n = 7
x = 4
formula for number of combinations is 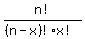
this winds up being 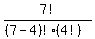
which becomes:
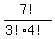
which becomes:
7*6*5*4*3*2*1/1*2*3*1*2*3*4
which becomes:
35
-----
The possible number of subsets = 35.
Each subset will not contain the same elements as any other subset.
Order is not important.
-----
3) How many different groups of 35 cars can be formed from 40 cars?
this looks like combinations again, since different groups would not contain the same cars in each group in a different order.
formula would be 
this becomes:
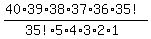 which equals 658008 which equals 658008
-----
4) How many different ways can an executive committee of nine people sit at a round table?
This should be permutations again.
It is similar to the beads question but only this time we have 9 executives instead of 11 beads.
Your answer should be 9! = 9*8*7*6*5*4*3*2*1 = 362,880.
-----
5) What is the probability of not drawing a green marble from a jar containing 7 red, 4 green, 3 white, and 9 blue marbles?
there are 4 green marbles in the set.
the probability of not drawing a green marble should be 1 - the probably of drawing a green marble.
the total marbles in the set are 7+4+3+9 = 23.
since there are 4 marbles in the set, the probability of drawing a green marble is 4/23.
therefore, the probability of not drawing a green marble should be 1 - 4/23 = 19/23.
another way of looking at it is:
the probability of not drawing a green marble is the probability of drawing any marble that is not green.
out of the 23 marbles, 19 of them are not green (7 red + 3 white + 9 blue), so the probability of drawing a marble that is not green is 19/23.
-----
6) A compound experiment consists of drawing at random twice without replacing from a jar with 3 red, 3 white, and 2 black marbles. What is the probability of getting first a red and then a black marble?
you start off with 3 red 3 white 2 black marlbes for a total of 8 marbles.
on your first draw, the probability of drawing a red marble is 3/8.
assuming you got the red marble you were looking for, then the probability of getting a black marble on the second draw is 2/7. the reason for this is that you got the red marble on the first draw and didn't return it into the pot so what was left was 2 red 3 white 2 black marbles.
----
now, the probability of event A happening and then event B happening is the p(A) * p(B) which means that the probability of first getting a red and then getting a black would be 3/8 * 2/7 = 6/56.
-----
you can look at that as follows: 3/8 of the time you get a red. within that 3/8 of the time, 2/7 of the time you get a black on the second draw.
getting them both can only happen 3/8 * 2/7 of the time.
try smaller number again to see what's happening.
you have a pot with 3 letters in it.
a,b,c
what is the probability of getting an (a) and then a (b)?
you will get the (a) 1/3 of the time.
once you get the (a), you will get the (b) 1/2 of the time, assuming you didn't return the (a) into the pile.
the possible combinations in order of how they were drawn is as follows:
ab
ac
ba
bc
ca
cb
the only successful draw would be ab which represents 1/6 of the total possible combinations.
1/3 * 1/2 = 1/6 so the formula of p(a) * p(b) is good and the answer for this example is 1/6.
It is not, however, the answer to the last question. It is only the answer to the example I just used.
the answer to your last question is 6/56 as I indicated above.
|
|
|