|
Question 202458: Can anyone help me with these problems please?
1) Use the matrix method to solve:
5x + 3y = 3
2x - 6y = 30
x = ____
y = ____
2) Perform the following operations on matrices.
(4) + (8) = (____)
(7) (2) (____)
3) Perform the following operations on matrices.
(1 8)(7 6) = (___ ___)
(0 7)(7 4) (___ ___)
Thank you in advance for all your help.
~Sarah
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
First, convert the system

into the matrix equation

So what we now need is inverse matrix of  to isolate to isolate 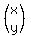
| Solved by pluggable solver: Finding the Inverse of a 2x2 Matrix |
To find the inverse of the matrix  , we can follow these steps: , we can follow these steps:
Step 1) Find the determinant
The determinant of  is is  . So this means that . So this means that 
Step 2) Swap the values
Now switch the highlighted values  to get to get 
Step 3) Change the sign
Now change the sign of the highlighted values  to get to get 
Step 4) Multiply by the inverse of the determinant
Multiply by  to get to get 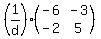
Plug in  to get to get 
Step 5) Multiply 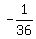 by every element in the matrix (simplify and reduce if possible) by every element in the matrix (simplify and reduce if possible)
Multiply 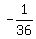 by EVERY element to get by EVERY element to get 
Multiply to get 
Reduce each element: 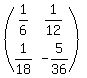
=================================================================
Answer:
So the inverse of  is is 
This means that if  then then 
|
Now left multiply both sides by the inverse matrix to get



So this means that  and and 
Note: let me know if you need help with matrix multiplication.
# 2
Simply add the corresponding components:

So 
# 3
Since the first matrix is a 2 by 2 matrix and the second matrix is a 2 by 2 matrix, this means that the resulting matrix will be a 2 by 2 matrix.
So the final resulting matrix will look like:
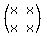
note: the "x"s are just placeholders for now
--------------------------------------------------
Multiply the corresponding entries from the 1st row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:
1st row, 1st column: 

So the element in the 1st row, 1st column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
Multiply the corresponding entries from the 1st row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:
1st row, 2nd column: 

So the element in the 1st row, 2nd column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:
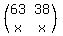
================================================================================
Multiply the corresponding entries from the 2nd row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:
2nd row, 1st column: 

So the element in the 2nd row, 1st column of the resulting matrix is 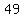 . Now let's update the matrix: . Now let's update the matrix:
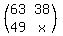
--------------------------------------------------
Multiply the corresponding entries from the 2nd row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:
2nd row, 2nd column: 

So the element in the 2nd row, 2nd column of the resulting matrix is 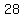 . Now let's update the matrix: . Now let's update the matrix:

==============================================================================
Answer:
So the solution is 
In other words,

|
|
|
| |