SOLUTION: Can ANYONE help me with ANY of these? 1) Use the rules of exponents to evaluate or simplify. Write without negative exponents. 3*4^0 = ____ 2) Use the rules of expo

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Can ANYONE help me with ANY of these? 1) Use the rules of exponents to evaluate or simplify. Write without negative exponents. 3*4^0 = ____ 2) Use the rules of expo      Log On


   

Question 202433: Can ANYONE help me with ANY of these?

1) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
3*4^0 = ____

2) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
1 / 4^-2 = ____

3) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
(1/4)^-1/2 = _____

4) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
(bm)^-3 = ____

5) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
y^-5 / y^-2 = ____

6) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
(-243)^3/5 = ____

7) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
36^1/2 = ____

Thank you for your help,
Sarah
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Let's review the rules of exponents. In these rules, the "variables" stand for any expression (unless there is a note to the contrary). They are numbered so they can be referred to by number, not because any of them are more important or useful than another.)
  1. A power of a power: %28a%5En%29%5Em+=+a%5E%28n%2Am%29
  2. Multiplication with the same base: a%5En+%2A+a%5Em+=+a%5E%28n+%2B+m%29 (Pay close attention to the difference between this rule and rule #1!)
  3. Division with the same base: %28a%5En%29%2F%28a%5Em%29+=+a%5E%28n+-+m%29
  4. Negative exponents: a%5E%28-n%29+=+1%2F%28a%5En%29 or 1%2F%28a%5E%28-n%29%29+=+a%5En. In words, a%5E%28-n%29 stands for the reciprocal of a^n.
  5. Zero exponents: a%5E0+=+1 Note: a must not be zero!
  6. Fractional exponents (where "n" and "m" are positive integers):
    • a%5E%281%2Fn%29+=++root%28n%2C+a%29. So a%5E%281%2F2%29+=+sqrt%28a%29 , a%5E%281%2F3%29+=+root%283%2C+a%29 , a%5E%281%2F4%29+=+root%284%2C+a%29 , etc.}}}
    • Using the above rule and rule #1 together: a%5E%28n%2Fm%29+=+%28+root%28m%2C+a%29%29%5En+=+root%28m%2C+a%5En%29
  7. The pseudo-distributive property. This property is not the distributive property but it does look a little like the distributive property: %28a%2Ab%29%5En+=+a%5En%2Ab%5En
  8. Exponents apply only to what is immediately in front of them! If the symbol immediately in front of an exponent is a grouping symbol, then the exponent is applied to the entire expression in the grouping symbol. Examples:
    • 4%5E2+=+4%2A4
    • -4%5E2+=+-%284%2A4%29+=+-16
    • %28-4%29%5E2+=+%28-4%29%2A%28-4%29+=+16. Note the difference between this example and the previous one. Here a ")" is right in front of the exponent. So the exponent applies to everything in the parentheses. In the previous example, a "4" is right in front of the exponent. So the exponent applies only to the 4 (and not the "-"!)
    • x+%2B+3%5E2+=+x+%2B+3%2A3+=+x+%2B+9
    • %28x+%2B+3%29%5E2+=+%28x+%2B+3%29%2A%28x+%2B+3%29+=+x%5E2+%2B6x+%2B9

Now let's try to solve your problems.
1) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
3*4^0 = ____
According to PEMDAS (the order of operations) we need to simplify the exponent before doing the multiplication. So we need to figure out 4^0 first. Using rule #5 we find that 4^0 = 1. Substituting this in we get
3*1 = ____
which, of course, is 3.

2) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
1 / 4^-2 = ____
Using the 2nd variation of rule #4:
1%2F%284%5E%28-2%29%29+=+4%5E2+=+16

3) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
(1/4)^-1/2 = _____
Using rule #1, in "reverse", we can rewrite this as:
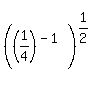
%28%281%2F4%29%5E%28-1%29%29%5E%281%2F2%29
Then, using rule #4, the expression in the parentheses can be simplified: %281%2F4%29%5E%28-1%29+=+4%5E1+=+4. Substituting we get:
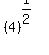%284%29%5E%281%2F2%29 which, according to rule #6, is sqrt%284%29+=+2

4) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
(bm)^-3 = ____
Using rule #1 again we can rewrite this as:
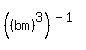
%28%28bm%29%5E3%29%5E%28-1%29
Using rule 7:
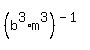
%28b%5E3%2Am%5E3%29%5E%28-1%29
Using rule #4:
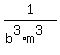
1%2F%28b%5E3%2Am%5E3%29

5) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
y^-5 / y^-2 = ____
Using rule #3
y%5E%28-5%29%2F%28y%5E%28-2%29%29+=+y%5E%28%28-5+-+%28-2%29%29%29+=+y%5E%28-3%29
Using rule #4 we get
y%5E%28-3%29+=+1%2Fy%5E3

6) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
(-243)^3/5 = ____
Using the second variation of rule #6:
%28-243%29%5E%283%2F5%29+=+%28root%285%2C+-243%29%29%5E3
Since %28-3%29%5E5+=+-243 root%285%2C+-243%29+=+-3. Substituting into the above we get
%28-3%29%5E3+=+-27

7) Use the rules of exponents to evaluate or simplify. Write without negative exponents.
36^1/2 = ____
Using rule #6
36%5E%281%2F2%29+=+sqrt%2836%29+=+6