SOLUTION: Open-top box. Thomas is going to make an open-top box by cutting equal squares from the four corners of an 11 inch by 14 inch sheet of cardboard and folding up the sides. If the

Click here to see ALL problems on test

Question 202324This question is from textbook Elementary and Intermediate Algebra
: Open-top box. Thomas is going to make an open-top box
by cutting equal squares from the four corners of an
11 inch by 14 inch sheet of cardboard and folding up the
sides. If the area of the base is to be 80 square inches, then
what size square should be cut from each corner? This question is from textbook Elementary and Intermediate Algebra

Found 4 solutions by stanbon, scott8148, MathTherapy, solver91311:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website!
Thomas is going to make an open-top box
by cutting equal squares from the four corners of an
11 inch by 14 inch sheet of cardboard and folding up the
sides. If the area of the base is to be 80 square inches, then
what size square should be cut from each corner?
---------------
Draw a picture of the 80 sq. in sqare.
----------------------------------------------
Cut an x by x square out of each corner of the cardboard
--------------------
Since the cardboard was a square with area 80 sq. in,
each side was sqrt(80) = 4sqrt(5)
----------------------
Fold the sides up to form a height of "x" for the box.
---------------------------
The base of the box is a square with side = 4sqrt(5)-2x
---------------------------
The Volume of the box = x[4sqrt(5)-2x] = -2x^2 +4sqrt(5)x
----------------------------------
This is a quadratic with a = -2, b = 4sqrt(5)
---------------------
The maximum volume occurs when x = -b/2a = -4sqrt(5)/-4 = sqrt(5)
----------------------------
So the square you cut out of each corner should have a side of
length sqrt(5).
===================================
Cheers,
Stan H.

Answer by scott8148(6628)   (Show Source):
You can put this solution on YOUR website!
let x="side of the square"

11 * 14 - 4x^2 = 80 ___ 74 = 4x^2 ___ 37/2 = x^2 ___ sqrt(37/2) = x

Answer by MathTherapy(10551)   (Show Source):
You can put this solution on YOUR website!
Since we�re using an 11�� by 14,� or 154 square-inch cardboard sheet, and since the base, or bottom of the box is going to be 80 square inches, after we form the bottom, or base of the box, we will have 74 (154 � 80) square inches remaining from the cardboard sheet.

This 74 square inches of cardboard will need to form 4 squares, or the sides of the box. Therefore, 4 squared sides of 18.5 (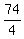) squared inches, each, will need to be cut from each of the 4 corners of the cardboard sheet.

Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website!

Let represent the measure of the side of one of the cut-out squares. Since each of the dimensions of the original piece of cardboard will be reduced by to form the base of the box, the dimensions of the base of the box will be and . Since the area of a rectangle is length times width and we know the area of the base must be 80 square inches, we can write:

Multiply the binomials and collect like terms:

This does not factor conveniently, so use the quadratic formula:

Both roots are real and positive, but one of them is way too large, namely meaning that the cutout squares would overlap and you would have no box at all. So exclude this root as extraneous having been introduced by the act of squaring the variable. The other root, is the correct answer.

John