Question 202316: find (a)the directrix, (b)the focus, and (c)the roots of the parabola
y = x^2 - 5x + 4
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! find (a)the directrix, (b)the focus, and (c)the roots of the parabola

We have to get it in the form

 Swap sides:
Swap sides:
 Add -4 to both sides the get the x-terms alone on the left.
Add -4 to both sides the get the x-terms alone on the left.
 Multiply the coefficient of x, which is
Multiply the coefficient of x, which is  by by  This gives
This gives  . Now we square . Now we square  and get and get  We add
We add  to both sides: to both sides:
 Factor the left side, and write the
Factor the left side, and write the  as as 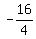
 Write the left side as the square of a binomial,
combine the fractions on the right:
Write the left side as the square of a binomial,
combine the fractions on the right:
 Now so that equation will look like this:
Now so that equation will look like this:
 we put the right side in parentheses and put a 1
coefficient before the parentheses, like this:
we put the right side in parentheses and put a 1
coefficient before the parentheses, like this:
 Now we can compare it to the equation:
Now we can compare it to the equation:
 and get
and get  , so , so 
 , so , so  So the vertex is (
So the vertex is ( , , ) or ( ) or ( , ,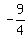 )
And )
And  , so , so  Now let's begin by plotting the vertex, which is (
Now let's begin by plotting the vertex, which is ( , , ),
But for plotting purposes, mixed numbers are better
than improper fractions, so for plotting vertex ( ),
But for plotting purposes, mixed numbers are better
than improper fractions, so for plotting vertex ( , ,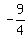 ),
we rewrite it as ( ),
we rewrite it as ( , ,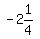 ) )
 Now we will find the x-intercepts, by settng
Now we will find the x-intercepts, by settng  in the original equation, and finding the "roots":
in the original equation, and finding the "roots":



 , so , so 
 , so , so  So the x-intecepts are (1,0) and (4,0)
So we plot those:
So the x-intecepts are (1,0) and (4,0)
So we plot those:
 and sketch in the parabola:
and sketch in the parabola:
 Now the focus is p units from the vertex INSIDE
the parabola, so since the parabola opens upward,
we add P or
Now the focus is p units from the vertex INSIDE
the parabola, so since the parabola opens upward,
we add P or  to the y-coordinate of the
vertex. Since the vertx is ( to the y-coordinate of the
vertex. Since the vertx is ( , ,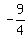 ),
the focus = ( ),
the focus = ( , , ) = ( ) = ( , ,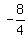 )
= ( )
= ( , , )
So we draw that point: )
So we draw that point:
 Now the directrix is a line OUTSIDE the parabola which is
also p-units, or
Now the directrix is a line OUTSIDE the parabola which is
also p-units, or  from the vertex.
Since the y-coordinate of the vertex is from the vertex.
Since the y-coordinate of the vertex is 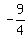 we want
the directrix to be we want
the directrix to be  unit below the vertex, so we
subtract unit below the vertex, so we
subtract  So the directrix is the horizontal line whose equation is
So the directrix is the horizontal line whose equation is
 . I'll draw it in in green: . I'll draw it in in green:
 So the focus is the POINT (
So the focus is the POINT ( , , ) and the
directrix is the LINE ) and the
directrix is the LINE  The "roots" are really the y-coordinates of the
x-intercepts or 1 and 4.
Edwin
The "roots" are really the y-coordinates of the
x-intercepts or 1 and 4.
Edwin
|
|
|