Question 202233: A broadway theatre has 500 seats, divided into orchestra, main, and balcony seating. Orchestra seats sell for $40, main seats for $25, and balcony seats for $20. If all the seats are sold, the gross revenue to the theatre is $13,150. If all the main and balcony seats are sold, but only half the orchestra seats are sold, the gross revenue is $11,150. How many are there of each kind of seat?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A Broadway theater has 500 seats, divided into orchestra, main, and balcony seating.
Orchestra seats sell for $40, main seats for $25, and balcony seats for $20.
If all the seats are sold, the gross revenue to the theatre is $13,150.
If all the main and balcony seats are sold, but only half the orchestra seats are sold,
the gross revenue is $11,150.
How many are there of each kind of seat?
:
Let x = Orchestra seats
Let y = Main seats
Let z = Balcony seats
:
Write an equation for each statement:
:
"A Broadway theater has 500 seats, divided into orchestra, main, and balcony seating."
x + y + z = 500
:
"Orchestra seats sell for $40, main seats for $25, and balcony seats for $20.
If all the seats are sold, the gross revenue to the theatre is $13,150."
40x + 25y + 20z = 13150
:
"but if only half the orchestra seats are sold, the gross revenue is $11,150."
40(.5x) + 25y + 20z = 11150
20x + 25y + 20z = 11150
:
use elimination on these two equations
40x + 25y + 20z = 13150
20x + 25y + 20z = 11150
-------------------------subtraction eliminates y and z
20x = 2000
x = 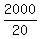
x = 100 orchestra seats
:
Using this value for x, write two equations with two unknowns.
100 + y + z = 500
y + z = 500 - 100
y + z = 400
and
40(100) + 25y + 20z = 13150
4000 + 25y + 20z = 13150
25y + 20z = 13150 - 4000
25y + 20z = 9150
:
Multiply the 1st equation by 20 and subtract from the above equation
25y + 20z = 9150
20y + 20z = 8000
-------------------subtraction eliminates z
5y = 1150
y = 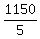
y = 230 Main seats
:
Find the number of Balcony seats using the total seat equation:
100 + 230 + z = 500
z = 500 - 330
z = 170 Balcony seats
;
;
Check our solutions by finding the total revenue
40*100 = 4000
25*230 = 5750
20*170 = 3400
-------------
total = 13150; confirms our solutions
;
;
Did this make sense to you?
|
|
|