Question 202134: Hello,
I need some help on quadratic equations. Any and all help will be appreciated.
1. Solve using the quadratic formula: x^2 - 3x = 4x -1
2. Solve using the quadratic formula: x^2 -5x - 1 = -7
3. Solve by completing the square: x^2 + 8x + 2 = 0
Thank you in advance for your help.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the quadratic formula is:
x = 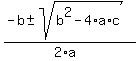
-----
the general form of the quadratic equation is:

-----
to use the quadratic equation, you find the values for a, b, and c, and plug them into the quadratic equation and solve.
-----
your first problem is:

first you need to convert it to the standard form.
subtract 4x from both sides of the equation and add 1 to both sides of the equation to get:

a = 1
b = -7
c = 1
plug these values into the quadratic equation to get:
x = 
which becomes:
x = 
this answer works as is but you can reduce it further by simplifying the number under the square root sign as follows:
x = 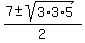
which reduces to:
x = 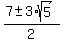
all you need to do now is verify the answer is correct by plugging those values for x into the original equation to see if the equation is true. I cheated by using my calculator, but the answers are verified to be true so these answers are good.
-----
your second problem is:
x^2 -5x - 1 = -7
-----
you do the same thing.
convert it to standard form.
get the values of a, b, and c.
plug them into the formulas and solve.
-----
i'll solve without explanation this time and you can follow along or try to solve it on your own.
x^2 - 5x - 1 = -7
add 7 to both sides to get:
x^2 - 5x + 6 = 0
-----
a = 1
b = -5
c = 6
x = 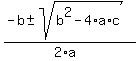
x = 
which becomes
x = 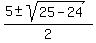
which becomes
x = 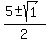
which becomes
x = 
which becomes
x = 3 or x = 2
-----
plug these values into the original equations to see if the equations are true.
original equation is:
x^2 -5x - 1 = -7
when x = 2 this becomes
4 - 10 - 1 = -7
which becomes
-6-1 = -7 which is true.
when x = 3 this becomes
9 - 15 - 1 = -7
which becomes
-6 -1 = -7 which is also true.
the answers are good.
x = 
-----
your last equation needs to be solved by completing the squares.
this is a different technique but gets you to the same answer.
you could also use the quadratic equation here as well, but sometimes completing the square is easier.
-----
your last equation is:

you would subtract 2 from both sides of the equation to get:

you take 8/2 = 4 and use that value to complete the square.
you take 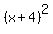 to get: to get:
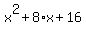 . .
so what you have is:
 . .
if you subtract 16 from that, you have:

you can now go back to your original equation after modification which was:

and substitute 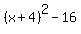 for for 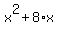 to get: to get:

you add 16 to both sides of the equation to get:

you have just completed the square.
solving by taking the square root of both sides and you will get:
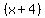 = +/- = +/- 
which becomes:

you verify that this answer is valid by plugging it into the original equation which was:

the values check out ok so the answer is good.
note that if you had solved this equation using the quadratic formula, you would have gotten the same answer.
-----
note that the standard form of the quadratic equation is:
 . .
to complete the square, you need to move the c over to the right side and you need to divide both sides of the equation by a, if a is not already 1.
-----
you will wind up with:

before dividing by a if it is not 1 to start with.
if a is not one, you will wind up with:

which is the same as:

-----
i'll show you how that works with a simple example.
once you have the standard form for completing the square, the operations are the same as above.
-----
take 
this is the standard form of the quadratic equation of  . .
note that a is not = to 1
first step:
move the c over to the right hand side by subtracting it from both sides of the equation.
you get:

-----
since the a coefficient is not 1 (it's 3), you need to divide both sides of the equation by 3 to make it 1.
it becomes:

which becomes:

-----
now you're in the standard form for completing the square.
-----
take 1/2 the b factor which means take 1/2 of 3.
you get 3/2
your factor that will be squared is 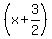 . .
-----
you get:

your left side of the equation was 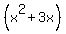
this equals 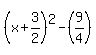
your equation which was:
 becomes: becomes:

you add (9/4) to both sides to get:

this becomes:

which becomes:

take the square root of both sides to get:
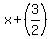 = +/- = +/- 
this means:

or

or
x = both.
you wind up with:
x = -1 or x = -2 or both.
both values of x checked out in the original equation so they're both good.
-----
|
|
|