|
Question 201858: Can someone please help me with this problem:
Find the lump sum deposited today that will yield the same total amount as this yearly payment(made at the end of each year for 20 years at the given intrest rate, compounded annually)
$10,700 at 8%
a. $102,758.52
b. $105,022.64
c. $107,179.76
d. $105,054.15
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! they want to know that if you took a loan out today for 20 years at 8% interest compounded annually, how much would the loan have been for.
for example:
I take a loan out today of $1000.
The loan charges 8% a year.
I take the loan out for 3 years.
How much do I have to pay back each year so that at the end of the 3 years the loan is paid off.
each payment will be part interest and part principal.
the bank keeps the interest.
the principal is taken off the amount of money I borrowed.
some real numbers to work with:
The loan is $1,000
The interest rate is 8%.
The period of the loan is 3 years.
My payment would be $388.033514 per year.
It is made at the end of each year.
Here's how it works.
Loan is $1000
Balance at the end of the first year before payment is $1080.
Balance at the the end of the first year after payment is $691.97.
Balance at the end of the second year before payment is $747.33.
Balance at the end of the second year after payment is $359.29.
Balance at the end of the third year before payment is $388.033514
Balance at the end of the third year after payment is $0.00
Each year the interest is added to increase the remaining balance and the payment is made to reduce the remaining balance.
I told you what the loan was and calculated the payment.
They're telling you what the payment was and want you to calculate the loan amount that the payment is for.
In order to solve this, you either need a financial calculator or you need to get the formula for the present worth of an annuity assuming an end of year payment.
You can also use Microsoft Excel if you have it.
I'll give you the formula here.
The formula for a present worth of a standard annuity with end of year payments is:

In your problem, PV is what you are looking for (Present Value) which is the equivalent for the loan amount.
PMT is the yearly payment.
i is the interest rate per year.
n is the number of years.
All you have to do is plug in the correct value and work the formula as follows:
PV = ?????
i = .08 per year (8%).
PMT = $10,700 per year payable at the end of each year.
n = 20 years.
The formula becomes:

This becomes:

which becomes:

which becomes:
PV = 105054.1773.
Your answer is D). $105,054.15 which is the closest to this answer.
they probably did some rounding during the intermediate calculations.
I just used the numbers that were stored in the calculator.
Now, the future worth of this amount, compounded annually for the next 20 years would equal to $489,653.0182 as shown below using the annual compounding of a present amount formula:
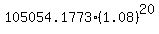 = 489653.0182 = 489653.0182
This is the exact same amount as the future worth of the annuity for 20 years.
The annuity is $10,700 per year deposited at the end of the year for 20 years at 8% a year. 105054 is the present worth of that annuity. 489653 is the future worth of that annuity.
There are formulas for the future worth of an annuity also. Those formulas are shown in the following Web Address shown below which contains other information and exercises as well. The formulas are not too far down in the presentation (maybe a couple of paragraphs or so).
http://www.college-cram.com/study/finance/presentations/1116
I used the financial calculator.
The key to this type of problem is the Present Value of the annuity is the equivalent amount of the investment today, and the Future Value of the annuity is the equivalent amount of the investment tomorrow.
20 years of payments at $10,700 a year for 20 years is the equivalent to investing $105k today and leaving it in the bank for 20 years. At the end of the 20 years, the $105k invested today would equal the same amount as the $10,700 invested at the end of each year.
|
|
|
| |