Question 201016: If there is anyone that can help me solve this or I should say these problems it would be a huge help I have a exam that I'm studying for and cant spend any more time tring to get the solutions. Thank you to anyone nice enough to help me out!
#1a)The sum of the squares of two numbers is 128. The product of the numbers is 64. Find the numbers? (answer with a exact solution and in ordered pairs)
#1b) The difference between the squares of two numbers is 3. Twice the square of the first number increased by the square of the second number is 9. Find the numbers? (please put your solutions in the form of an ordered pair(s)
#1c) A 150 ffet of fence is available to enclose a 1125 square foot region in the shape of adjoining squares. With the sides of length X and Y. The big square has sides of length X and the small square has sides of length Y. Find X and Y?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll do the first two to get you going in the right direction.
a)
"The sum of the squares of two numbers is 128" translates to 
"The product of the numbers is 64" translates to 
 Start with the second equation. Start with the second equation.
 Divide both sides by "x". Divide both sides by "x".
 Move onto the first equation Move onto the first equation
 Plug in Plug in 
 Square Square 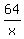 to get to get 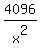
 Multiply EVERY term by the LCD Multiply EVERY term by the LCD  to clear out the fractions. to clear out the fractions.
 Subtract Subtract 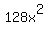 from both sides. from both sides.
 Rearrange the terms. Rearrange the terms.
Let  . So . So 
 Replace Replace  with with  . Replace . Replace  with with 
Notice that the quadratic 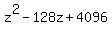 is in the form of is in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for "z":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate 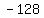 to get to get  . .
 Square Square 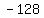 to get to get  . .
 Multiply Multiply 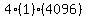 to get to get 
 Subtract Subtract  from from  to get to get 
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of  to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the only solution (in terms of "z") is 
Now recall that we let  . So this means that . So this means that  and that and that  or or 
--------------------------
Now let's find "y" when  : :
 Go back to the first isolated equation. Go back to the first isolated equation.
 Plug in Plug in 
 Reduce. Reduce.
So when  , ,  giving the ordered pair (8,8) giving the ordered pair (8,8)
--------------------------
Now let's find "y" when  : :
 Go back to the first isolated equation. Go back to the first isolated equation.
 Plug in Plug in 
 Reduce. Reduce.
So when  , ,  giving the ordered pair (-8,-8) giving the ordered pair (-8,-8)
===============================================================
Answer:
So the two ordered pair solutions are (8,8) and (-8,-8)
b)
"The difference between the squares of two numbers is 3" translates to 
"Twice the square of the first number increased by the square of the second number is 9" translates to 
 Start with the first equation. Start with the first equation.
 Add Add  to both sides. to both sides.
 Move onto the second equation. Move onto the second equation.
 Plug in Plug in 
 Distribute Distribute
 Subtract 6 from both sides. Subtract 6 from both sides.
 Combine like terms. Combine like terms.
 Divide both sides by 3. Divide both sides by 3.
 Reduce Reduce
 or or  Take the square root of both sides (don't forget the "plus/minus") Take the square root of both sides (don't forget the "plus/minus")
 or or  Take the square root of 1 to get 1 Take the square root of 1 to get 1
--------------------------
Now that we know "y", we can use these values to find "x".
Let's find "x" when  : :
 Start with the given equation. Start with the given equation.
 Plug in Plug in 
 Square 1 to get 1 Square 1 to get 1
 Combine like terms. Combine like terms.
 or or  Take the square root of both sides Take the square root of both sides
So the first two ordered pair solutions are (2,1) and (-2,1)
--------------------------
 Start with the given equation. Start with the given equation.
 Plug in Plug in 
 Square 1 to get 1 Square 1 to get 1
 Combine like terms. Combine like terms.
 or or  Take the square root of both sides Take the square root of both sides
So the next two ordered pair solutions are (2,-1) and (-2,-1)
========================================================
Answer:
So the four ordered pair solutions are:
(2,1), (-2,1), (2,-1) and (-2,-1)
c)
I'll let you do this one on your own. Let me know if you have questions.
If you have any questions, email me at jim_thompson5910@hotmail.com.
Check out my website if you are interested in tutoring.
|
|
|