SOLUTION: please help with step by step 3x^2-6x over x^3+2x^2 divided by -x^2-2x+8 over x^4+6x^3+8x^2

Algebra ->  Expressions-with-variables -> SOLUTION: please help with step by step 3x^2-6x over x^3+2x^2 divided by -x^2-2x+8 over x^4+6x^3+8x^2      Log On


   

Question 200967: please help with step by step 3x^2-6x over x^3+2x^2 divided by -x^2-2x+8 over x^4+6x^3+8x^2
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
The first set of steps will
  • Reduce the first two fractions by canceling out a common factor. These reduced fractions will make the rest of the problem easier.
  • Multiply the top and bottom of the second fraction (for reasons which will become clear later)
  • Factor the third denominator

Starting with 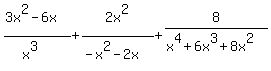%283x%5E2-6x%29%2F%28x%5E3%29%2B2x%5E2%2F%28-x%5E2-2x%29%2B8%2F%28x%5E4%2B6x%5E3%2B8x%5E2%29
Factor out x from the numerator and denominator of both the first two fractions and factor out the GCF of the third denominator:

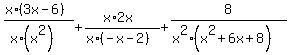
Cancel out the factors of x in the numerators and denominators of both the first two fractions and factor 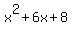x%5E2%2B6x%2B8 in the third denominator
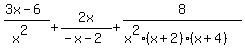
%283x-6%29%2F%28x%5E2%29%2B2x%2F%28-x-2%29%2B8%2F%28x%5E2%28x%2B2%29%28x%2B4%29%29
Now multiply the top and bottom of the second fraction by -1
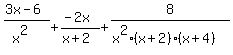
%283x-6%29%2F%28x%5E2%29%2B%28-2x%29%2F%28x%2B2%29%2B8%2F%28x%5E2%28x%2B2%29%28x%2B4%29%29

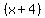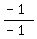Now we are ready to try to add the fractions. Of course we need a common denominator. The LCD will be the product of all the different factors of all the denominators: x%5E2, %28x%2B2%29 and %28x%2B4%29. (See why we multiplied the second fraction by %28-1%29%2F%28-1%29?)

To change the denominators to the LCD we will multiply the numerator and denominator of each fraction by the factors of the LCD which it does not already have:

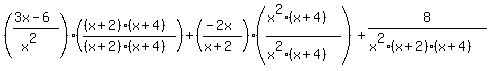
Multiply out the numerators (and leave the denominators factored).

Add the fractions (combining only like terms, of course)
%28-2x%5E4-5x%5E3%2B12x%5E2-12x-40%29%2F%28%28x%5E2%29%28x%2B2%29%28x%2B4%29%29
Next we should try to factor the numerator to see if there a factors in common with the factors of the denominator. But as far as I can tell the numerator will not factor. This means one of the following

  • The answer is %28-2x%5E4-5x%5E3%2B12x%5E2-12x-40%29%2F%28%28x%5E2%29%28x%2B2%29%28x%2B4%29%29
  • I incorrectly interpreted the problem
  • The numerator of %28-2x%5E4-5x%5E3%2B12x%5E2-12x-40%29%2F%28%28x%5E2%29%28x%2B2%29%28x%2B4%29%29 really does factor. (NOTE: Since x or x^2 are clearly not factors, the only factors that will be of any use would be (x+2) or (x+4))
  • An error was made above and %28-2x%5E4-5x%5E3%2B12x%5E2-12x-40%29%2F%28%28x%5E2%29%28x%2B2%29%28x%2B4%29%29 is not actually correct because of an error in the work above.

If I started with the wrong problem, perhaps you can learn from what I've done and figure out the correct answer. If not, then repost the question and put parentheses around each numerator, each denominator and around entire fractions like:
  ((numerator)/(denominator)) + ((numerator)/(denominator)) + ...
If I got the problem right then check my work above for errors and also see if the numerator of the answer can be divided evenly by (x+2) or (x+4).