Question 200686: The number of ways one can select three cards from a group of n cards (assuming the order of the selection matters), where n>3 P(n)=n^3-3n^2+2n , is given by . For a certain card trick a magician has determined that there are exactly 60 ways to choose three cards from a given group. How many cards are in the group?
Answer by Edwin McCravy(20060)   (Show Source):
You can put this solution on YOUR website! The number of ways one can select three cards from a group of n cards (assuming the order of the selection matters), where 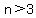  , is given by . For a certain card trick a magician has determined that there are exactly 60 ways to choose three cards from a given group. How many cards are in the group?
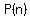Substitute  for  and solve for  :
Switch sides of the equation:
Get 0 on the right by subtracting 60 from both sides:
The possible rational zeros of P(n) are ± the divisors of
60.
±1, ±2, ±3, ±4, ±5, ±6, ±10, ±12, ±15, ±30, ±60
Try 1 using synthetic division:
1 | 1 -3 2 -60
| 1 -2 0
------------
1 -2 0 -60
Nope
Try 2 using synthetic division:
2 | 1 -3 2 -60
| 2 -2 0
------------
1 -1 0 -60
Nope
Try 3 using synthetic division:
3 | 1 -3 2 -60
| 3 0 6
------------
1 0 2 -54
Nope
Try 4 using synthetic division:
4 | 1 -3 2 -60
| 4 4 24
------------
1 1 6 -36
Nope
Try 5 using synthetic division:
5 | 1 -3 2 -60
| 5 10 60
------------
1 2 12 0
That leaves a 0 remainder, so n=5 is a solution
So we have factored the polynomial equation
as
This gives
 and 
There can be no positive solutions of
since there are
no sign changes.
So the answer is n=5.
Edwin
|
|
|
