|
Question 200660: Hi all I asked a similiar question recently and got a reaaly good response, but this imiliar problem is still giving me trouble.
I need to solve the following Matrices and comment on the outcomes.For the following:
A =
(2 3 0)
1 4 -3
B =
(1 -1 4)
2 3 5
C =
(2 -1)
3 5
Find and state why or why not the following is possible.
i) A+B
ii) C^-1
iii) AB
1v) B^C
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Table of Contents:
Part i)
Part ii)
Part iii)
Part iv)
Given Matrices:



Jump to Top of Page
Part i)
 Start with the addition of the two given matrices Start with the addition of the two given matrices
 Add up the matrices by adding the corresponding entries Add up the matrices by adding the corresponding entries
 Add Add
===========================================
Answer:
So 
Jump to Top of Page
Part ii)
To find the inverse of the matrix  , we can follow these steps: , we can follow these steps:
Step 1) Find the determinant
The determinant of 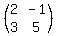 is is  . So this means that . So this means that 
note: since the determinant is NOT equal to zero, the matrix inverse exists.
--------------------------------
Step 2) Swap the values
Now switch the highlighted values  to get to get 
--------------------------------
Step 3) Change the sign
Now change the sign of the highlighted values 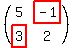 to get to get 
--------------------------------
Step 4) Multiply by the inverse of the determinant
Multiply by  to get to get 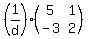
Plug in  to get to get 
--------------------------------
Step 5) Perform scalar multiplication and simplify.
Multiply  by EVERY element to get by EVERY element to get 
Multiply to get 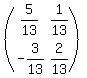
=================================================================
Answer:
So the inverse of 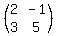 is is 
This means that if  then then 
note: to verify your work, multiply the matrices  and and 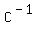 and you should get the matrix and you should get the matrix 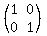 (the identity matrix). (the identity matrix).
Jump to Top of Page
Part iii)
Take note that the dimensions of matrices A and B are 2x3 and 2x3 respectively. Since the inner dimensions do NOT match, this means that the matrix product AB is NOT defined. In other words, AB does NOT exist.
note: if A and B are mxn and nxp matrices, then the product AB is defined. It is only defined if the number of columns of A equals the number of rows of B. Otherwise, AB does NOT exist.
===========================================
Answer:
So the matrix product AB is not defined (ie it doesn't exist).
Jump to Top of Page
Part iv)
I'm sure you meant to write 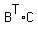 correct? If so, then... correct? If so, then...
Step 1: Transpose matrix B to get 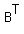 . You do this by converting each row into a column (and vice versa). . You do this by converting each row into a column (and vice versa).

Step 2: Multiply matrices 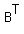 and C. Since the inner dimensions are equal, this means that the matrix product and C. Since the inner dimensions are equal, this means that the matrix product 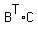 is defined. is defined.
Since the first matrix is a 3 by 2 matrix and the second matrix is a 2 by 2 matrix, this means that the resulting matrix will be a 3 by 2 matrix.
So the final resulting matrix will look like:

note: the "x"s are just placeholders for now
--------------------------------------------------
Multiply the corresponding entries from the 1st row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:
1st row, 1st column: 

So the element in the 1st row, 1st column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
Multiply the corresponding entries from the 1st row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:
1st row, 2nd column: 

So the element in the 1st row, 2nd column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

================================================================================
Multiply the corresponding entries from the 2nd row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:
2nd row, 1st column: 

So the element in the 2nd row, 1st column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
Multiply the corresponding entries from the 2nd row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:
2nd row, 2nd column: 

So the element in the 2nd row, 2nd column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

================================================================================
Multiply the corresponding entries from the 3rd row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:
3rd row, 1st column: 

So the element in the 3rd row, 1st column of the resulting matrix is 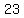 . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
Multiply the corresponding entries from the 3rd row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:
3rd row, 2nd column: 

So the element in the 3rd row, 2nd column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

==============================================================================
Answer:
So 
In other words,

Jump to Top of Page
|
|
|
| |