|
Question 200482: Hi everyone I asked a similiar question recently but got no responce, I may have input the question incorrectly.
I need to solve the following Matrices and comment on the outcomes.
For the following:
A =
( 2 -1 1 )
1 1 -2
B =
( 1 -1 )
2 3
C =
( 1 -1 )
0 1
-2 1
Find and state why or why not the following is possible.
i) A^T + C
ii) AB
iii) CB
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! 


i)
Step 1: Find the transpose of A to get 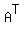

Step 2: Add 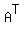 to C (just add up each component) to get to C (just add up each component) to get



=================================
Answer:
So 
ii) The product AB is NOT possible since the dimensions of A are 2x3 and the dimensions of B are 2x2. The inner dimensions MUST match for matrix multiplication to be defined.
So  does not exist. does not exist.
iii)
Since the first matrix is a 3 by 2 matrix and the second matrix is a 2 by 2 matrix, this means that the resulting matrix will be a 3 by 2 matrix.
So the final resulting matrix will look like:

note: the "x"s are just placeholders for now
Multiply the corresponding entries from the 1st row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:
1st row, 1st column: 

So the element in the 1st row, 1st column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
Multiply the corresponding entries from the 1st row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:
1st row, 2nd column: 

So the element in the 1st row, 2nd column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
================================================================================
Multiply the corresponding entries from the 2nd row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:
2nd row, 1st column: 

So the element in the 2nd row, 1st column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
Multiply the corresponding entries from the 2nd row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:
2nd row, 2nd column: 

So the element in the 2nd row, 2nd column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
================================================================================
Multiply the corresponding entries from the 3rd row of the first matrix by the 1st column of the second matrix. After multiplying, add the values:
3rd row, 1st column: 

So the element in the 3rd row, 1st column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
Multiply the corresponding entries from the 3rd row of the first matrix by the 2nd column of the second matrix. After multiplying, add the values:
3rd row, 2nd column: 

So the element in the 3rd row, 2nd column of the resulting matrix is  . Now let's update the matrix: . Now let's update the matrix:

--------------------------------------------------
==============================================================================
Answer:
So 
In other words, 
|
|
|
| |