SOLUTION: This is about vectors find the magnitude and the direction of the resultant of vector y(7,0) and vector z(0,6). I found the magnitude already,=SquareRoot of 85 What would be th

Click here to see ALL problems on Geometric formulas

Question 200276: This is about vectors
find the magnitude and the direction of the resultant of vector y(7,0) and vector z(0,6).
I found the magnitude already,=SquareRoot of 85
What would be the Direction?
Do I have to graph the resultant, AND THEN find the direction by making a right triangle?
Found 2 solutions by jim_thompson5910, solver91311:
Answer by jim_thompson5910(35256) (Show Source):
You can put this solution on YOUR website!
Well I'm sure that you know to add the components of the two vectors (how else did you get the magnitude?) to get (7+0, 0+6) ---> (7,6). So the resultant vector is (7,6)

To find the direction, you need to find the argument (or the angle between the x-axis and the vector). For any vector (a,b), the angle "x" is

So simply compute the arctangent of 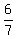to find the angle.

To graph the resultant, first graph the two given vectors and then add the resultant in (through the use of the parallelogram method or the head-to-tail method).

Answer by solver91311(24713) (Show Source):
You can put this solution on YOUR website!

Your vectors are orthogonal to the axes, so the end point of the resultant is simply the -coordinate of your vector and the -coordinate of your vector , in other words . You are correct in saying that the magnitude of the resultant is because . The direction of the resultant is the angle the resultant makes with the x-axis or:

Read that as "the angle whose tangent is 6 divided by 7".

Calculator: First decide whether you want your answer in degrees or radians, then set the calculator mode appropriately. I choose radians.

Keystrokes:

6

'divide'

7

'='

'inverse function mode'

'tan'

Result: approximately 40.6 radians.

John