SOLUTION: solve the given polynomial equation, use rational zero theorem and Descrates rule of sighns as an aid in optaining the first root to begin synthetic division to give the solution s

It has 1 sign change going from left to right.
so it has 1 positive zero, which means it
has either 2 or 0 negative zeros.

The only rational zeros it might have are the
fractions whose numerators divide evenly into
the last term and whose denominators divide
evenly into the first coefficient, 8.

So the only possible rational zeros are

±1/1. ±1/2, ±1/4, ±1/8

or

±1. ±1/2, ±1/4, ±1/8
 
We try 1

1 | 8 -10 -7  -1
  |     8 -2  -9 
   -------------
    8  -2 -9 -10

No luck.  We try 1/2

1/2 | 8 -10  -7 -1
    |     4  -3 -5 
     ---------------
      8  -6 -10 -6

No luck.  We try 1/4

1/4 | 8 -10 -7    -1
    |     2 -2  -9/4 
     ---------------
      8  -8 -9 -13/4

No luck.  We try 1/8

1/8 | 8 -10    -7      -1
    |     1  -9/8  -65/64 
     --------------------
      8  -9 -65/8 -129/64

No luck.  We try -1

-1 | 8 -10 -7  -1
   |    -8 18 -11 
   --------------
     8 -18 11 -12

No luck.  But, we learned that since the signs 
on that bottom row alternate and we are looking 
for a negative zero, that -1 is a lower bound
for the negative zeros.  But heck, the only
possibilities of a rational zero are greater 
than -1 anyway. So, that didn't really help.

We try -1/2

-1/2 | 8 -10 -7 -1
     |    -4  7  0 
     ---------------
       8 -14  0 -1

No luck.  We try -1/4

-1/4 | 8 -10 -7 -1
     |    -2  3  1 
     --------------
       8 -12 -4  0

Hey yeah! -1/4 is a zero

So now we have factored the original
polynomial equation this way:



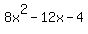So now we factor the  by taking
out 4. 







Setting each factor = 0:


  
     we already knew that was one.



, , 

 







So there are three zeros:

, , and 
 
Edwin