Question 199510This question is from textbook Using and Understanding Mathematics A Quantitative Reasoning Approach
: Suppose you arrive at a bus stop randomly, so all arrival times are equally likely. The bus arrives regularly every 30 minutes without delay, (say on the hour, every half-hour). What is the expected value of your waiting time?
This question is from textbook Using and Understanding Mathematics A Quantitative Reasoning Approach
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose you arrive at a bus stop randomly, so all arrival times are equally likely. The bus arrives regularly every 30 minutes without delay, (say on the hour, every half-hour). What is the expected value of your waiting time?
Half the time you will arrive at the bus stop during the 15 minute period after the last bus left, and half the time you'll arrive during the 15 minute period before the next bus arrives.
For instance, you'll arrive at the bus stop, say, 6 minutes after the last bus left, (in which case your wait will be 24 minutes) just as often as you'll arrive at the bus stop 6 minutes before the next bus comes (in which case your wait will be 6 minutes). The average of those two waiting times, 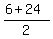 is 15 minutes. is 15 minutes.
In general, you'll arrive at the bus stop n<15 minutes after the last bus left, (in which case your wait will be n+15 minutes) as often as you'll arrive at the bus stop n<15 minutes before the next bus comes (in which case your wait will be 15-n minutes). The average of those two waiting times,  is also 15 minutes. is also 15 minutes.
So it's quite obvious that your average waiting time will be 15 minutes, and
that is what is meant by "expected" waiting time.
Edwin
|
|
|