Question 199508: A 45-foot rope is to be cut into three pieces. The second piece must be twice as long as the first piece and the third peice must be 9 feet longer than 3 times the length of the second piece. How long should each three peices be?
How do I write this problem algibraicly? How do I solve it? My Final is tomarrow please help.
-Andrew
Found 2 solutions by jim_thompson5910, Electrified_Levi:
Answer by jim_thompson5910(35256)   (Show Source):
Answer by Electrified_Levi(103) (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
A 45-foot rope is to be cut into three pieces. The second piece must be twice as long as the first piece and the third peice must be 9 feet longer than 3 times the length of the second piece. How long should each three peices be?
How do I write this problem algibraicly? How do I solve it? My Final is tomarrow please help.
-Andrew
.
So the total amount of rope is 45 ft, so, that means the length of all three rope lengths will equal 45
.
We have to name the lengths in terms of "x"
.
You can usually name one of the variables, in this case there are three, "x", it probably doesn't matter, but we will use the easiest way
.
We will name Length 1, "x"
.
The second piece must be twice as long as the first piece,
.
If the length 1 is "x", and length 2 has to be twice as long, length 2 = "2x"
.
We will work the third piece a little slower, because it is the hardest of the three
.
the third peice must be 9 feet longer than 3 times the length of the second piece,
.
the third peice must be 9 feet longer than 3 times the length of the second piece, which is "2x"
.
the third peice must be 9 feet longer than 3 times "2x"
.
the third peice must be 9 feet longer than 3(2x)
.
the third peice must be 9 feet longer than "6x",
.
You would now add "9" to "6x"
.
the third peice must be "6x + 9",
.
Length 3 = "6x + 9"
.
.
.
Length 1 =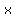 
.
Length 2 =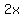 
.
Length 3 =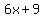 
.
All of these lengths will add up to 45, we can now have our equation
.
.
We can get rid of the parentheses
.
.
Now add like terms
.
= 
.
We will move "9" to the right side
.
=  =  , to find "x" divide each side by "9"
.
=  =  , you can check your answer by replacing "x" with "4" in the equation
.
=  =  =  =  ( True )
.
.
Length 1 = =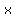 
.
Length 2 = =  =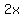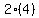 
.
Length 3 = =  =  =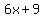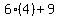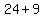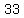 
.
To show you that you can make "x" any of the lengths, I will briefly do "x" as the Length 2
.
Length 2 = , if length 2 is twice length 1, then length 1 = 
, Length 3, is 9 more than three times the second's length, or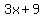 
.
Length 1 =
.
Length 2 =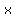
.
Length 3 =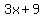
.
You would then add these to equal 45 again
.
 , you would solve to find "x" = 8, which was length 2
.
.
Length 1 = =  =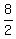
.
Length 2 = =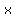
.
Length 3 = =  = =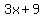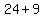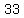
.
If you even wanted to have Length 3 = "x" you could, but that would be the hardest and most difficult.
.
Length 1 =
.
Length 2 =
.
Length 3 =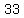
.
Hope I helped, Levi
|
|
|
